
Cargando...
¿Qué puedo hacer?
226539 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Acerca de este recurso...
Índice
Definición y propiedades de la matriz traspuesta.
La mayor aplicación práctica de la matriz traspuesta es el cálculo de la matriz inversa.
La matriz traspuesta de una matriz se denota por A^T y se obtiene cambiando sus filas por columnas (o viceversa).
Ejemplo:
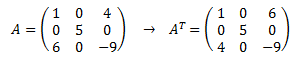
Obsérvese, por ejemplo, que la primera fila de la matriz A es (1,0,4). Esta fila es la primera columna de su matriz traspuesta.
Sea A una matriz de dimensión mxn, denotamos al elemento de la fila i y columna j como A(i,j), siendo i<m y j<n. Entonces, se define la matriz traspuesta de A como la matriz A^T de dimensión nxm tal que A^T(j,i) = A(i,j), siendo i<m y j<n.
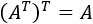
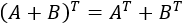
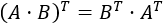
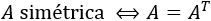
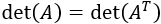
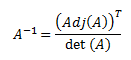
Contenido exclusivo para miembros de

Mira un ejemplo de lo que te pierdes
Categorías:
Etiquetas:
Fecha publicación: 18.4.2018
Se respeta la licencia original del recurso.
¿Quieres comentar? Regístrate o inicia sesión
Añadir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0