
Cargando...
¿Qué puedo hacer?
226539 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Acerca de este recurso...
Recordad que un sistema de ecuaciones lineales (SEL) puede representarse de forma matricial como A·X = b, donde A es la matriz de coeficientes, X es la matriz columna de incógnitas y b es la matriz columna de términos independientes. Recordad que el SEL es
El teorema de Rouché-Frobenius establece la relación entre el rango de la matriz ampliada (A|b) del sistema A·x = b y el tipo de sistema.
El teorema dice:
"Sea el sistema A·X=b con m ecuaciones lineales y con n incógnitas, donde m y n son naturales mayores que 0. Entonces,
El sistema AX = b es compatible si, y sólo si, rango(A) = rango(A|b)
El sistema AX = b es compatible determinado si, y sólo si, rango(A) = rango(A|b)= n"
Ejemplo de aplicación:
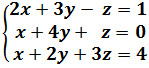
La matriz ampliada del sistema es:
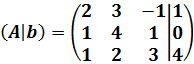
El rango de la matriz es
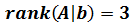
ya que tiene un determinante de dimensión 3 no nulo:
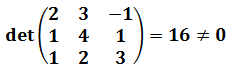
Además, como el determinante anterior también es el determinante de la matriz A, la matriz de coeficientes también tiene rango 3:
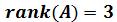
Por tanto, tenemos que los rangos de las dos matrices coinciden
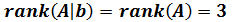
y, por el teorema de Rouché-Frobenius, como el rango es igual al número de incógnitas, el sistema es compatible determinado.
En efecto, la única solución del sistema es, en forma matricial,
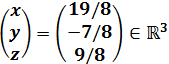
Es decir,
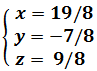
Nota: la solución se ha calculado por la regla de Cramer.
Más ejemplos: Teorema de Rouché-Frobenius
Otros temas relacionados:
Contenido exclusivo para miembros de

Mira un ejemplo de lo que te pierdes
Categorías:
Etiquetas:
Fecha publicación: 16.4.2018
Se respeta la licencia original del recurso.
¿Quieres comentar? Regístrate o inicia sesión
Añadir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0