
Cargando...
Que pode fazer?
226539 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Sobre este recurso...
En este texto vamos a ver cómo multiplicar dos matrices, pero antes recordaremos la suma de matrices y el producto de un número por una matriz.
Lo primero que diremos con la intención de que lo aprendamos cuanto antes es
La suma de matrices es fácil de calcular y exige que las matrices que se suman tengan la misma dimensión (mismo número de filas y de columnas).
La suma de matrices se calcula sumando los elementos que ocupan la misma posición.
Ejemplo:

Antes de ver el producto de dos matrices veamos el producto de un número por una matriz:
El producto de un número α por una matriz A es la matriz que resulta al multiplicar por α todos los números de A. Este producto sí es conmutativo.
Ejemplo: (producto por un número y suma)

El producto de matrices es un poco más complicado de calcular. Si se quiere multiplicar la matriz A por la matriz B, el número de columnas de A tiene que coincidir con el número de filas de B.
El resultado del producto A·B es una matriz que tiene el mismo número de filas que A y el mismo número de columnas que B.
Observad que
Veamos cómo se calcula:
Supongamos que el número de columnas de A coincide con el número de filas de B.
Entonces, el elemento de la fila i y columna j de la matriz A·B es el producto de la fila i de A por la columna j de B.
Para verlo más claro nos ayudaremos de un ejemplo:
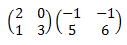
Llamaremos A a la matriz de la izquierda y B a la de la derecha. Estas matrices son de dimensión 2x2, por lo que podemos calcular el producto AB que será una matriz de dimensión 2x2.
(2,0)·(-1,5) = 2·(-1) + 0·5 = - 2
(2,0)·(-1,6) = 2·(-1) + 0·6 = - 2
(1,3)·(-1,5) = 1·(-1) + 3·5 = -1 + 15 = 14
(1,3)·(-1,6) = 1·(-1) + 3·6 = -1 + 18 = 17
Por tanto, el producto es
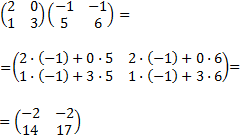
Ejemplo 2: producto de dos matrices rectangulares

La matriz A·B tiene dimensión 2x2.
Ejemplo 3: producto de dos matrices cuadradas de dimensión 3

La matriz A·B tiene dimensión 3x3.
Más información:
Matriz inversa (1)
Calculadoras online de matrices:
Conteúdo exclusivo para membros de

Mira un ejemplo de lo que te pierdes
Categorias:
Etiquetas:
Fecha publicación: 28.2.2018
Respeita a licença original do recurso.
Deseja fazer um comentário? Registrar o Iniciar sessão
Si ya eres usuario, Inicia sesión
Adicionar ao Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0