
Cargando...
Que pode fazer?
226539 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Sobre este recurso...
Un hexágono regular es un hexágono cuyos lados y ángulos miden lo mismo. Los ángulos (interiores) miden 120º.
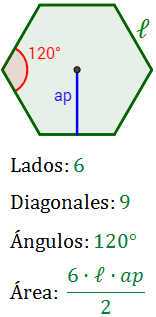
Un pentágono regular tiene 9 diagonales y su área es
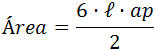
donde L es la medida del lado y ap la del apotema (segmento que une el centro del pentágono con el punto medio de cualquiera de sus lados).
Problema 1: Si el lado de un hexágono regular mide 6cm y su apotema mide 5.2cm,¿cuál es el perímetro y el área de dicho hexágono?
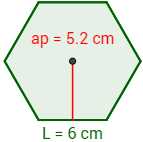
Solución:
Los datos que tenemos son el lado y la apotema:
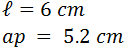
El perímetro es la suma de las longitudes de todos los lados. Como el hexágono es regular, todos sus 6 lados miden lo mismo, así que su perímetro es
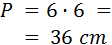
La fórmula del área del hexágono regular es
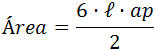
Como tenemos el lado y la apotema, sólo tenemos que sustituirlos en la fórmula:
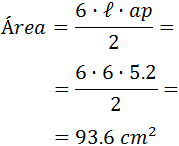
Nota: no olvidemos que las unidades del área son al cuadrado.
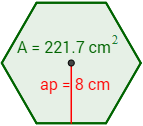
Problema 2:Calcular el perímetro de un hexágono
regular si tiene un área de 221.7cm2 y su apotema mide 8cm.
Solución:
El perímetro de un hexágono regular es
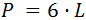
donde L es la longitud del lado. No sabemos cuánto mide el lado, pero conocemos el área y la apotema. Podemos aislar el lado de la fórmula del área
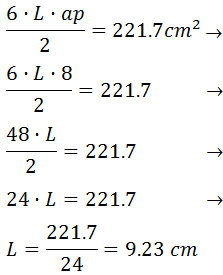
Luego el lado mide 9.23cm y, por tanto, el perímetro es
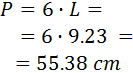
Enlaces de geometría 2D:
Clasificación de triángulos II (interactivo): equilátero, isósceles y escaleno
Elementos del triángulo I (interactivo): altura, mediana y bisectriz
Elementos del triángulo II (interactivo): ortocentro, baricentro e incentro
Ángulos I (interactivo): Amplitud de ángulos: nulo, agudo, recto, obtuso, llano y perigonal
Áreas de figuras con formas circulares (problemas resueltos)
Trigonometría básica: seno, coseno y tangente (problemas resueltos)
Otros:

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Conteúdo exclusivo para membros de

Mira un ejemplo de lo que te pierdes
Categorias:
Etiquetas:
Fecha publicación: 18.5.2017
Respeita a licença original do recurso.
Deseja fazer um comentário? Registrar o Iniciar sessão
Si ya eres usuario, Inicia sesión
Adicionar ao Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0