
Cargando...
Que puis-je faire ?
226307 materialEducativo
textoFiltroFichatipo de documento Matematiques - Tutorial
À propos de cette ressource...
Una ecuación de segundo grado es una ecuación polinómica cuyo grado es 2, es decir, aquella en la que el grado mayor de los monomios es 2 (es decir, su parte literal es x al cuadrado).
Toda ecuación de segundo grado puede escribirse como
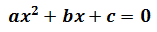
Los números a, b y c son los coeficientes de la ecuación, siendo siempre a distinto de 0 (si no, no sería una ecuación de segundo grado).
Las ecuaciones de segundo grado se clasifican en ecuaciones completas y ecuaciones incompletas. Un ecuación es completa cuando los tres coeficientes a, b y c son distintos de 0. Si b ó c son 0, entonces es incompleta.
Para calcular la solución o soluciones debemos aplicar la siguiente fórmula:
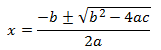
Ejemplo:
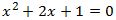
En esta ecuación los coeficientes son a = 1, b = 2 y c = 1. Aplicamos la fórmula:
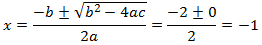
Esta ecuación sólo tiene una solución. Esto se debe a que el radicando de la fórmula es 0.
Al radicando de la fórmula (el interior de la raíz) se denomina discriminante de la ecuación:
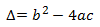
Según el signo del discriminante, la ecuación tendrá dos soluciones, una solución o ninguna solución:
La ecuación es incompleta si b = 0 ó c = 0. Por tanto, hay tres tipos de ecuaciones incompletas:
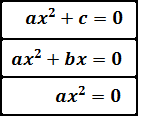
La ecuación es de la forma
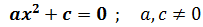
Despejando tenemos que
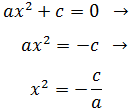
Haciendo la raíz cuadrada, obtenemos las dos soluciones
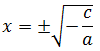
Pero es necesario que el radicando (interior de la raíz) sea positivo. Si no es así, no existen soluciones (reales).
Ejemplo:
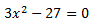
Despejamos x y hacemos la raíz cuadrada (no olvidemos el doble signo)
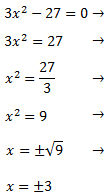
La ecuación tiene dos soluciones: x = 3, x = - 3.
La ecuación es de la forma
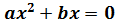
Factorizamos
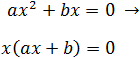
Como es un producto cuyo resultado es 0, alguno de los dos factores tiene que ser 0. Por tanto, tenemos las siguientes posibilidades (raíces):
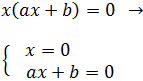
Una solución es x = 0 y la otra es x = -b/a.
Ejemplo:
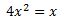
Factorizamos la expresión y nos queda un producto de x por un polinomio de primer grado:
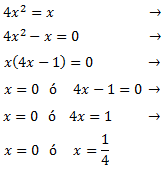
La ecuación tiene dos soluciones: x = 0, x = 1/4.
La ecuación es de la forma
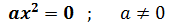
Tenemos la única solución: x = 0.
Enlaces:
 Esta obra está bajo una licencia Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Esta obra está bajo una licencia Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Contenu exclusif pour les membres de

Mira un ejemplo de lo que te pierdes
Autores:
Catégories:
Étiquettes:
Fecha publicación: 9.2.2017
Contenu sous licence de Creative Commons Attribution 3.0 License. 
Que se passe t’il ? Inscrivez-vous ou lancer session
Si ya eres usuario, Inicia sesión
Ajouter à Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Commenter
0