Definición y propiedades de las matrices triangulares.

Una matriz triangular puede ser triangular superior o triangular inferior. Llamaremos simplemente matriz triangular a una matriz triangular superior o inferior (porque tienen propiedades comunes).

Matriz triangular superior

Una matriz triangular superior es una matriz cuyos elementos por debajo de la diagonal son 0.

Ejemplos:



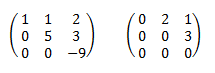
La segunda matriz del ejemplo tiene también los elementos de la diagonal igual a 0.

Definición formal: Si llamamos A(i,j) al elemento de la matriz A, entonces A es triangular superior si A(i,j)=0 para todo i>j (donde i y j toman los valores adecuados según la dimensión de A).

Matriz triangular inferior

Una matriz triangular inferior es una matriz cuyos elementos por encima de la diagonal son 0.

Ejemplos:



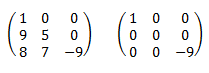
Obsérvese que la segunda matriz del ejemplo es triangular inferior y triangular superior. Esto ocurre cuando la matriz es diagonal.

Definición formal: Si llamamos A(i,j) al elemento de la matriz A, entonces A es triangular inferior si A(i,j)=0 para todo i<j (donde i y j toman los valores adecuados según la dimensión de A).

Propiedades de las matrices triangulares

• La matriz traspuesta de una triangular superior es triangular inferior y viceversa.
• Si la matriz es cuadrada, su determinante es el producto de los elementos de la diagonal. Por tanto, una matriz triangular es regular cuando los elementos de su diagonal son no nulos.
• La inversa de una matriz triangular superior (inferior) es una matriz triangular superior (inferior).
• El producto de matrices triangulares superiores (inferiores) es una matriz triangular superior (inferior).
• Los autovalores (valores propios) de una matriz cuadrada triangular son los elementos de la diagonal.

Algunas de estas propiedades se demuestran en la página Problemas teóricos sobre matrices.

Enlaces de Álgebra Matricial:

• Conceptos básicos de Matrices
• Matrices Equivalentes: operaciones elementales y formas escalonadas
• Concepto de la matriz inversa: definición, propiedades y métodos
• Matrices Especiales: identidad, diagonal, triangular, traspuesta, adjunta, simétrica, definida positiva, diagonalmente dominante, Hessenberg
• Sistemas de Ecuaciones y Matrices (teoría)
• Determinante, Rango y Menores de una Matriz y Teorema de Rouché-Frobenius
• Diagonalización de Matrices
• Suma de matrices y Matriz Transpuesta
• Producto de Matrices
• Potencias de Matrices
• Matriz Inversa por Adjunción
• Determinantes de matrices con parámetros
• Ejercicios teóricos de matrices (demostraciones)