
Cargando...
What can I do?
226539 materialEducativo
textoFiltroFichatipo de documento Mathematics - Tutorial
About this resource...
En esta sección vamos a ver cómo construir autómatas finitos (deterministas y no deterministas y con y sin pila) a partir de expresiones regulares o de la propia definición del lenguaje.
Recordamos al lector que las expresiones regulares son una forma de representar un lenguaje (regular). Veamos algunos ejemplos:
0(11)*
El lenguaje de esta expresión regular lo conforman las palabras que empiezan por 0 seguidas de un número par de 1's (el asterisco significa que la subcadena a la que enierra puede repetirse tantas veces como se desee).
La palabra w = 0 también es una palabra de dicho lenguaje y corresponde al caso en que la subcadena 11 se repite 0 veces.
(1+0)1*
El lenguaje está formado por las palabras que empiezan por 0 o por 1 (el signo + representa la unión, es decir, o uno u otro) y que están seguidas (o no) por 1's.
PROBLEMA 1
Dado el alfabeto Σ={0,1}, construir un Autómata Finito Determinista de 4 estados como máximo, que acepte el lenguaje representado por la siguiente expresión regular ((01+10)(11)∗0)∗(01+10)(11)∗.
Solución:
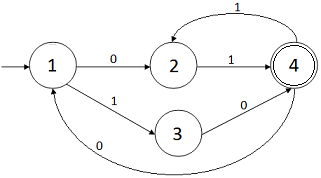
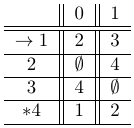
Tabla de la función de transición del AFD:
Exclusive content for members of

Mira un ejemplo de lo que te pierdes
Categories:
Tags:
Fecha publicación: 15.4.2018
The original license is kept.
Add to Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comment
0