
Cargando...
Was kann ich tun?
226523 materialEducativo
textoFiltroFichatipo de documento Mathematik - Lernprogramm
Über diese Ressource...
En esta página definimos sector circular y proporcionamos las fórmulas para calcular el área (en ángulos, en radianes y en función del arco) y el perímetro.
Un sector circular es la porción de un circulo delimitada por dos radios R y un arco de circunferencia L:
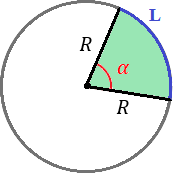
El ángulo α es el ángulo que hay entre los dos radios del sector (amplitud del ángulo central del sector). Si el ángulo es α=2π radianes (ó 360 grados), el sector circular es un círculo completo.
Tenemos 3 fórmulas para calcular el área de un sector circular. Dos de ellas dependen del ángulo α del sector (una en grados y la otra en radianes). La otra fórmula es en función de la longitud del arco L del sector.
Fórmula del Área en grados: Para el ángulo α en grados utilizamos la fórmula
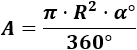
Fórmula del Área en radianes: Para el ángulo β en radianes utilizamos la fórmula
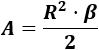
Fórmula del Área con longitud de arco: Si la longitud de arco del sector es L, entonces el área del sector es
El perímetro de un sector circular es la suma de los radios R y de la longitud del arco L:
Recordatorio: la longitud del arco de circunferencia con ángulo α∘ en grados es
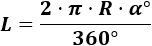
Y con ángulo β en radianes es
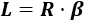
Problema 1
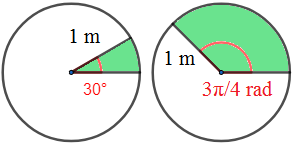
Calcular el área del sector circular de una circunferencia de radio 1 metro y ángulo
Problema 2
Calcular el perímetro de los sectores circulares del problema anterior.
Problema 3
Calcular en grados y en radianes el ángulo del sector circular con área igual a 6πcm^2 de un circulo cuyo perímetro es 4π√2⋅cm.
Problema 4
Demostrar la fórmula (con ángulo en grados) del área del sector circular a partir de la fórmula del área de un círculo (πR^2).
Problema 5
Demostrar la fórmula del área del sector circular con ángulo en radianes (utilizar la fórmula del Problema 4).
Soluciones: Sectores Circulares: área, perímetro y problemas resueltos
Otros recursos:
Exklusive Inhalte für Mitglieder von

Mira un ejemplo de lo que te pierdes
Kategorien:
Fecha publicación: 15.7.2018
Die Originallizenz der Ressource wird respektiert.
Möchtest du einen Kommentar abgeben? Registriere dich oder inicia sesión
Si ya eres usuario, Inicia sesión
Add to Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Kommentieren
0