
Cargando...
Was kann ich tun?
226539 materialEducativo
textoFiltroFichatipo de documento Mathematik - Lernprogramm
Über diese Ressource...
En esta página explicamos intuitivamente el concepto de límite de una función (de una variable: x), tanto en un punto finito como infinito.
Decimos que el límite de f(x) cuando x tiende al punto a es L si la función toma valores cada vez más cercanos a L cuando x toma valores cada vez más cercanos al punto a.
Lo expresamos mediante
Consideremos la función f(x) = x^2. Para calcular su límite en el punto x = 2, damos a valores cercanos a 2 por su izquierda y su derecha.
Por la izquierda:
Por la derecha:
Se observa que la función tiende a 4 por ambos lados de 2. Por tanto, su límite es 4:
Gráfica de la función:
Si la función tiende a puntos distintos por uno y otro lado del punto a, entonces no existe el límite de la función en dicho punto.
Observad que, normalmente, el límite de f(x) en el punto a coincide con su imagen, es decir, con f(a) . Para ser más exactos, esto ocurre en las funciones que son continuas en el punto a.
Un ejemplo de función discontinua es f(x) = 1/(x^2) , cuyo límite cuando x tiende a 0 no coincide con f(0) porque la función ni siquiera está definida en dicho punto (no podemos dividir entre 0).
Decimos que el límite de f(x) cuando x tiende a más infinito (+∞) es L si la función toma valores cada vez más cercanos a L cuando x crece indefinidamente.
Lo expresamos mediante
Análogamente, el límite de f(x) cuando x tiende a menos infinito (-∞) es L si la función toma valores cada vez más cercanos a L cuando x decrece indefinidamente.
Lo expresamos mediante
El límite de la función cuadrado es infinito:
Y el límite de su inverso es 0:
El límite es 0 porque un cociente positivo toma valores positivos más pequeños a medida que su denominador aumenta. Por tanto, cuando el denominador tiende a infinito, el cociente tiende a 0.
Gráfica de la función:
Más ejemplos
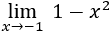
Los polinomios son funciones continuas, así que su límite en un punto finito a siempre es f(a).
Calculamos el límite sustituyendo el punto:
Gráfica de la función:
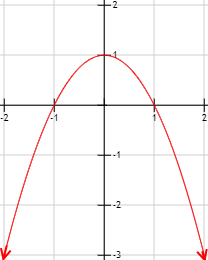
El límite de un polinomio cuando x tiende a infinito (positivo o negativo) siempre es infinito. El signo del infinito del límite depende el grado y del coeficiente principal del polinomio.
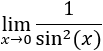
El seno de 0 es 0 y, por tanto, su cuadrado también es 0.
Como un cuadrado es siempre no negativo, el denominador tiende a 0 por ambos lados.
Cuando el denominador de una fracción positiva decrece, el cociente crece. Por tanto, cuando x se acerca a 0, la función toma valores muy grandes. Es decir, el límite es infinito:
Gráfica de la función:
Más ejemplos y temas de límites:
Exklusive Inhalte für Mitglieder von

Mira un ejemplo de lo que te pierdes
Kategorien:
Tags:
Fecha publicación: 10.6.2019
Die Originallizenz der Ressource wird respektiert.
Möchtest du einen Kommentar abgeben? Registriere dich oder inicia sesión
Si ya eres usuario, Inicia sesión
Add to Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Kommentieren
0