1. Dominio y codominio

Una función, f, es una ley entre dos conjuntos de números: el dominio y el codominio. A cada número del dominio le hace corresponder un único número del codominio. Esta ley es una correspondencia unívoca.

Ejemplo:

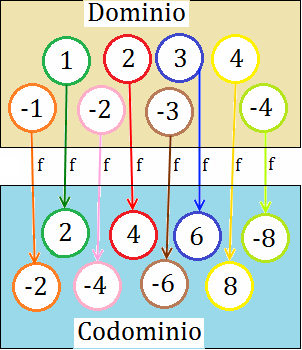
En el ejemplo, el dominio es el conjunto

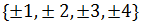
El codominio es el conjunto

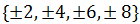
La expresión de la función es

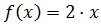
ya que lo que hace la función es multiplicar por dos cada número del dominio.

Podemos observar cómo a cada elemento del dominio le corresponde un único elemento del codominio.

2. Recorrido o Imagen

Sea x un elemento del dominio, llamamos imagen de x mediante la función f a f(x), es decir, al elemento del codominio que le asigna la función f.

En la función del ejemplo:

• La imagen de 1 es

  f(1) = 2·1 = 2

• La imagen de -1 es

  f(-1) = 2·(-1) = -2

• La imagen de 2 es

  f(2) = 2·2 = 4

• La imagen de -2 es

  f(2) = 2·(-2) = -4

• Es análogo para los restantes elementos del dominio.

Llamamos conjunto imagen (o simplemente imagen) o recorrido de la función f al conjunto de elementos del codominio que son la imagen de algún (o más) elemento del dominio.

Es decir, si y es un elemento de la imagen de f, entonces existe al menos un elemento, x, del dominio de f tal que

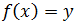
Nota: el conjunto imagen de una función es un subconjunto del codominio. En muchos textos no se realiza ninguna distinción entre los conceptos de codominio y recorrido (o imagen) y se utilizan ambos términos con el significado que le hemos dado al de recorrido (o imagen).

En el ejemplo anterior, el codominio coincide con la imagen.

Enlaces:

• Ejercicios de dominio y recorrido de funciones

• Ejercicios de la continuidad de funciones

• Tipos de funciones: inyectiva, sobreyectiva, biyectiva, función inversa.

• Foro de Ayuda

• Calcular porcentajes online

• Calcular Pitágoras online

• Problemas y Ecuaciones

• Ecuaciones Resueltas

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

Esta obra está bajo una licencia Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.