Didactalia: material educativo

Siguenos en redes sociales:

¿Qué puedo hacer?

buscador
Descubre
Carrito Total 0 0

226539 materialEducativo

textoFiltroFicha

Derivada de una función elevada a otra función

tipo de documento Matemáticas - Tutorial

Jose Llopis Jose Llopis

  • Me gusta 0
  • Visitas 60340
  • Comentarios 0
  • Guardar en
  • Acciones

Acerca de este recurso...

Índice

  1. 1. 2. Ejemplos de aplicación
    1. 1.1. Ejemplo 1:
  2. 2.  
  3. 3.  
  4. 4.  
  5. 5.  
  6. 6.  
  7. 7.  
  8. 8. 3. Enlaces relacionados

En este artículo vamos a obtener una fórmula para calcular la derivada de una función elevada a otra función, por ejemplo:

Derivada de una función elevada a otra función

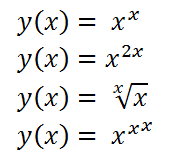
1. La fórmula

Sea la función y(x) la que queremos derivar. Supongamos que es de la forma:

Derivada de una función elevada a otra función

 

 

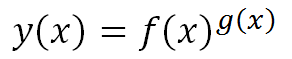
Es decir, la función y(x) es la función f(x) elevada a la función g(x).

Para facilitar la notación, escribimos y, f y g para referirnos a las funciones y(x), f(x) y g(x), respectivamente. Las derivadas de estas funciones las escribiremos como y', f' y g'.

Por tanto, la función es

Derivada de una función elevada a otra función

 

 

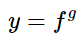
Aplicamos logaritmos y sus propiedades a la igualdad anterior:

 

Derivada de una función elevada a otra función

 

 

 

 

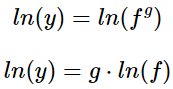
Derivamos en la igualdad (derivada del producto y del logaritmo) aplicando la regla de la cadena:

 

Derivada de una función elevada a otra función

 

 

 

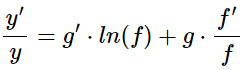
Aislamos y' en la expresión anterior:

Derivada de una función elevada a otra función

 

 

 

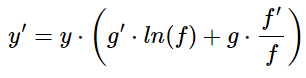
Esta última expresión es la fórmula que usaremos. Sólo tenemos que identificar las funciones f y g, calcular sus derivadas y aplicar la fórmula.

 

2. Ejemplos de aplicación

Ejemplo 1:

Calculamos la derivada de

Derivada de una función elevada a otra función

 

 

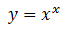
Aplicamos la fórmula:

Derivada de una función elevada a otra función

 

 

 

 

 

 

 

 

 

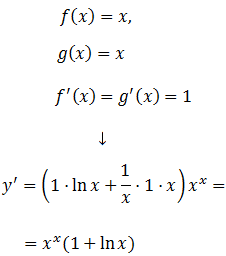
Ejemplo 2:

Calculamos la derivada de

Derivada de una función elevada a otra función

 

 

 

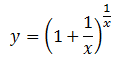
Aplicamos la fórmula:

Derivada de una función elevada a otra función

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3. Enlaces relacionados

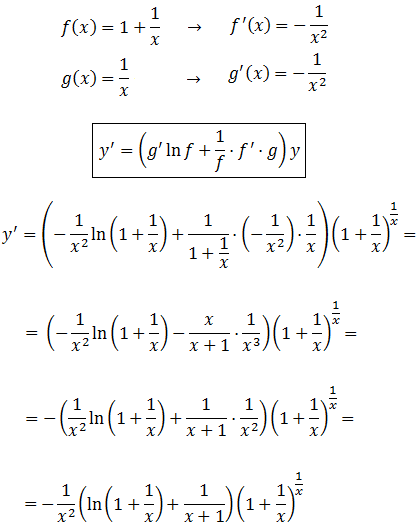
Cálculo diferencial:

Integración:

Álgebra matricial:

Otros: 

Ecuaciones Resueltas:

Logaritmos:

Licencia de Creative Commons

Esta obra está bajo una licencia Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Mapa Conceptual: Derivada de una función elevada a otra función

Contenido exclusivo para miembros de

D/i/d/a/c/t/a/l/i/a
Iniciar sesión

Mira un ejemplo de lo que te pierdes

Autores:

Categorías:

Etiquetas:

Fecha publicación: 9.2.2017

Contenido bajo una licencia de Creative Commons Attribution 3.0 License. Licencia Creative Commons

formatos disponibles

Comentar

0

¿Quieres comentar? Regístrate o inicia sesión

Únete a Didactalia

Navega entre 226539 recursos y 574047 usuarios

Regístrate >

O conéctate a través de:

Si ya eres usuario, Inicia sesión

¿Quieres acceder a más contenidos educativos?

Iniciar sesión Únete a una clase
x

Añadir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...

Ayuda del juego
Juegos de anatomía
Juega a aprender el cuerpo humano con Didactalia
Selecciona nivel educativo