
Cargando...
¿Qué puedo hacer?
226539 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Acerca de este recurso...
Los límites de las sucesiones se calculan aplicando los mismos razonamientos que en los límites de las funciones, pero en ocasiones estos razonamientos no son suficientes. Es entonces cuando empleamos los criterios de convergencia específicos para sucesiones.
El criterio de la media aritmética se utiliza para calcular límites de sucesiones del tipo
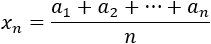
Si la sucesión a(n) tiende a A∈R∪{∞}, entonces la sucesión de sus medias aritméticas también tiende a A. Es decir,
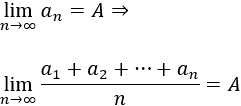
Nota: el criterio también es válido para A=∞.
Demostración en Criterio de la media aritmética.
Ejemplo 1
La sucesión a(n) = 1/n es convergente a 0. Por el criterio de la media aritmética, la siguiente sucesión también converge a 0:
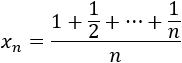
Ejemplo 2
La sucesión a(n) = ln(n) tienda a infinito. Por tanto, la siguiente sucesión también:
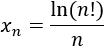
Criterios de convergencia:
Otros temas de sucesiones:
Otros:
Contenido exclusivo para miembros de

Mira un ejemplo de lo que te pierdes
Categorías:
Etiquetas:
Fecha publicación: 25.6.2018
Se respeta la licencia original del recurso.
¿Quieres comentar? Regístrate o inicia sesión
Añadir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0