
Cargando...
Que pode fazer?
224320 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Sobre este recurso...
En este texto vamos a calcular algunos límites de sucesiones. Los razonamientos que seguimos para el cálculo de límites de sucesiones son los mismos que los que seguimos para el de límites de funciones (una sucesión es una función definida sobre los naturales). Esto significa que en los límites de las sucesiones pueden aparecer indeterminaciones que ya sabemos cómo resolver: cálculo de límites e indeterminaciones.
Una sucesión a(n) es convergente a L≠∞ (L es finito) si
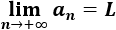
En este caso dice que la sucesión a(n) converge a su límite L y lo expresamos por a(n)→L. En caso contrario, la sucesión diverge. Aclaraciones:
Nota: hacemos las anteriores aclaraciones ya que, para nosotros, la divergencia es la no convergencia, así que una sucesión es convergente o divergente. Algunos consideran que la divergencia es tener límite infinito y, por tanto, una sucesión puede ser convergente (límite finito), divergente (límite infinito) o no convergente ni divergente (sin límite).
1. Límite de a(n) = 5/n
El límite de la sucesión es 0 porque el grado del denominador es mayor que el del numerador:
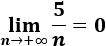
2. Límite de a(n) = 3 - 2/n
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
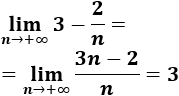
3. Límite de a(n) = n^2/(n + 1)
El límite de la sucesión es infinito porque el grado del numerador es mayor que el del denominador:
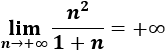
4. Límite de a(n) = (n^2 - 2)/(2n^2 - 1)
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
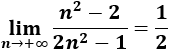
Límite 1
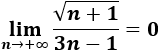
El grado del numerador es 1/2 y el del denominador es 1. Por tanto, tiende a 0.
Límite 2
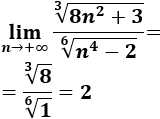
El límite es el cociente de los coeficientes directores porque el grado del numerador y el del numerador son el mismo (2/3 = 4/6).
Límite 3
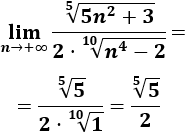
Finalmente, calculamos el límite de la sucesión
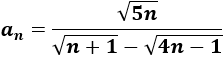
El grado del numerador y el del denominador son el mismo, pero tal y como está escrita la sucesión, no sabemos cuál es el coeficiente director del denominador. Tenemos que operar un poco (multiplicar y dividir por el conjugado del denominador):

Más ejercicios: Cálculo de límites de sucesiones o progresiones
Otros temas de progresiones:
Otros:
Conteúdo exclusivo para membros de

Mira un ejemplo de lo que te pierdes
Categorias:
Etiquetas:
Fecha publicación: 20.6.2018
Respeita a licença original do recurso.
Deseja fazer um comentário? Registrar o Iniciar sessão
Si ya eres usuario, Inicia sesión
Adicionar ao Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0