When the integrand is formed by a product (or a division, which we can treat like a product) it's recommended the use of the method known as integration by u-substitution, that consists in applying the following formula:

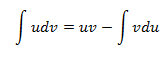
Even though it's a simple formula, it has to be applied correctly. Let's see a few tips on how to apply it well:

• Select u and dv correctly: A bad choice can complicate the integrand. Supposing we have a product, and one of the factors is monomial (x^3 for example). As a rule, we will call u all powers and logarithms; and dv exponentials, fractions and trigonometric functions (circular functions).

• Don't change our minds about the selection: Sometimes we need to apply the method more than once for the same integral. When this happens, we need to call u the result of du from the first integral we applied the method to. The same applies to dv. If we don't do this, seeing as choosing one option or another involves integration or differentiating, we'll be undoing the previous step and we won't be able to advance.

• Cyclic integrals: Sometimes, after applying integration by u-substitution twice we have to isolate the very integral from the equality we've obtained in order to resolve it. 

Example 1

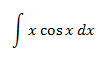
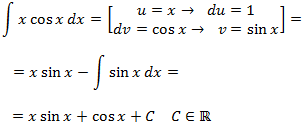
Notes: it doesn't matter if cos(x) in u or dv (due to the fact we obtain a sinus). We choose u = x to reduce it's degree (and that way x disappears). If we choose dv = x, we increase the degree.

Example 2

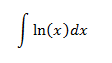
In this integral we don't have an explicit product of functions, but we don't know what the logarithms primitive function is, so we differentiate it, that way u = ln(x).

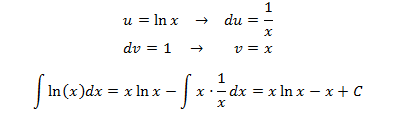
Example 3

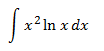
It's in our interest to select u = x2 (to reduce the exponent) but then we're forced that dv = ln(x) and obtaining v isn't immediate. So we'll select the other case

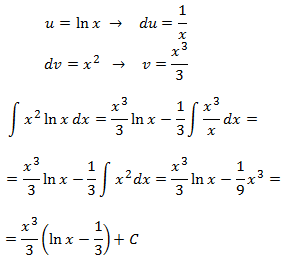
More examples: Integration by U-substitution: resolved integrals step by step

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.