Una potència és una expressió del tipus

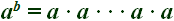
Aquesta potencia representa el resultat de multiplicar la base, a, per si mateixa tantes vegades com indica l'exponent, b. Ho llegim com "a elevat a b".

Exemple: potència 2 elevat a 5:

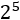
Per calcular-la, multipliquem la base (és 2) per si mateixa 5 vegades:

Propietats de les potències

1. Producte de dues potències (mateixa base):

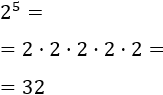
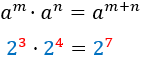
És a dir, es sumen els exponents.

2. Quocient de dues potències (mateixa base):

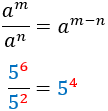
És a dir, es resten els exponents (el del numerador menys el del denominador).

3. Exponent negatiu:

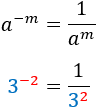
És a dir, el signe negatiu en l'exponent indica l'invers de la potència.

4. Potència d'una potència

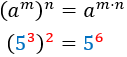
És a dir, la base es manté i els exponents es multipliquen.

5. Invers d'una fracció

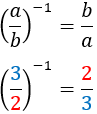
El resultat d'elevar a -1 és l'invers de la base.

Aquestes propietats s'empren tant de dreta a esquerra com d'esquerra a dreta. Per simplificar expressions amb potències, caldrà conèixer-les.

Exemples d'aplicació de les propietats de les potències

Exemple 1

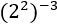
Primer apliquem la propietat de la potència d'una potència, així que hem de multiplicar ambdós exponents obtenint una potència amb exponent negatiu. Com l'exponent és negatiu, calculem l'invers:

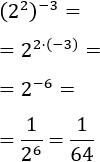
Exemple 2:

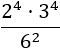
Tenim un producte de potències en el numerador però no podem calcular-lo al tenir bases distintes (2 i 3). En el denominador tenim una potència de base 6 que es pot escriure com 3·2.

Escrivim la potència del denominador com un producte de potències de bases 3 i 2 perquè així tindrem bases en comú i podrem aplicar les propietats:

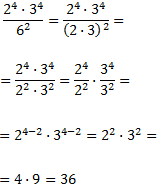
Al escriure la base del denominador com un producte amb les mateixes bases que en el numerador, podem aplicar les propietats de les potències per simplificar.

Exemple 3:

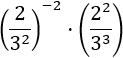
Primer, podem desfer-nos del signe negatiu de l'exponent de la primera potència escrivint l'invers de la fracció. D'aquesta manera, tindrem divisions de potències amb les mateixes bases.

Més exemples: Exercicis de simplificar potències.

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.