
Cargando...
Zer egin dezaket?
226539 materialEducativo
textoFiltroFichatipo de documento Matematika - Unitate didaktikoa
Baliabide honi buruz...
Definimos función inyectiva, función suprayectiva y función inversa.
Sea la función dada por
La imagen de -1 es 0, pero ¿cuál es la anti-imagen de 2 y la de 4?
Podemos resolver las ecuaciones f(x)=2 y f(x)=4, pero es más rápido si disponemos de la función inversa:
Calculamos las anti-imágenes de 2 y 4:
Gráfica de f:
Una función es inyectiva si las imágenes de elementos distintos son distintas. Es decir,
O bien,
Para comprobar que una función es inyectiva, se tiene que demostrar que si f(a)=f(b) entonces a=b.
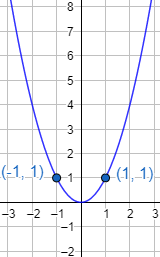
La función f(x)=2 no es inyectiva. Por ejemplo, las imágenes de 1 y -1 son iguales:
Gráfica:
Una función f es suprayectiva o sobreyectiva si todo elemento del codominio tiene anti-imagen. Es decir,
Esta propiedad depende del codominio: podemos definir el codominio para conseguir que una función sea suprayectiva.
La función f(x)=2x es suprayectiva:
Sea b un número, entonces, su anti-imagen es a=b/2 ya que
Por ejemplo, la anti-imagen de 9 es 9/2.
Una función f es biyectiva si es inyectiva y sobreyectiva.
Función inversa
Toda función biyectiva, f, tiene una función inversa, f – 1.
La función inversa es la función que cumple
Es decir,
La función f(x)=2x es biyectiva.
Comprobamos que la función f – 1(x) = x/2 es su inversa:
Para calcular la inversa seguimos los siguientes pasos:
1. Igualamos la expresión de la función a y.
2. Despejamos la incógnita x (así, queda en función de y).
3. Cambiamos la x por la y y viceversa. La expresión obtenida es la de la inversa.
Calculamos la inversa de la función
1. Igualamos a y:
2. Despejamos x:
3. Intercambiamos x por y:
Por tanto, la función inversa es
Enlaces con problemas de funciones:
Kide hauentzat bakarrik:

Mira un ejemplo de lo que te pierdes
Kategoriak:
Etiketak:
Fecha publicación: 10.12.2019
Baliabidearen jatorrizko lizentzia errespetatzen da.
Aipatu nahi al duzu? Erregistratu o Hasi saioa
Didactalia-ri Gehitzea Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Aipatu
0