Ecuaciones en diferencias finitas (EDF)

tipo de documento Matematika - Tutoriala

Jose Llopis

Gustatzen zait 1
Bisitak 518
Oharrak 0
Hemen gorde:
Ekintzak
- Lotura bidali

Baliabide honi buruz...

Una EDF (ecuación en diferencias finitas) de orden k es

Ecuaciones en diferencias finitas (EDF)

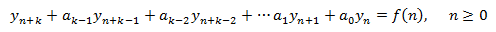
y diremos que una sucesión

Ecuaciones en diferencias finitas (EDF)

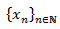
es solución si verifica la EDF, esto es, si

Ecuaciones en diferencias finitas (EDF)

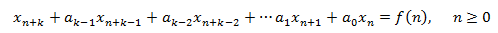
Diremos que la EDF es homogenia (EDFH) si

Ecuaciones en diferencias finitas (EDF)

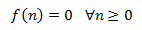
Definimos el polinomio característico de una EDF como

Ecuaciones en diferencias finitas (EDF)

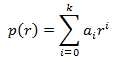
En esta página resolveremos ecuaciones en diferencias finitas (EDF) de primer y segundo orden no homogéneas.

Al igual que en otros tipos de ecuaciones, como las ecuaciones diferenciales, la solución de una EDF no homogénea es la suma de la solución de la homogénea y de una solución particular: x = x(h) + x(p)

Tanto en las de primer y segundo orden, para obtener la solución de la homogénea calcularemos el polinomio característico de la EDF. En el caso de las de segundo orden, éste será un polinomio de segundo orden, con lo que tendremos dos soluciones y habrá que distinguir los casos en que son reales distintas, real de multiplicidad doble o complejas.

Obviaremos el método o algoritmo para resolver las EDFs, que es extenso y podemos encontrar aquí, y sólo mostramos una tabla con las soluciones particulares típicas (la primera columna es el término independiente y la segunda la solución particular).