
Cargando...
What can I do?
226539 materialEducativo
textoFiltroFichatipo de documento Mathematics - Tutorial
About this resource...
El sistema hexadecimal es un sistema de numeración posicional de base 16.
Los símbolos que se usan en este sistema son:
Veamos el método para pasar del sistema decimal al sistema hexadecimal mediante un ejemplo. Escribiremos el número 460 (base 10) en base 16:
1. Dividimos el número entre 16:
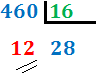
2. Si el cociente es mayor o igual que 16, lo dividimos entre 16.
En nuestro caso, el cociente es 28 (mayor que 16), con lo que lo dividimos de nuevo:
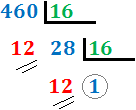
3. Continuamos así hasta obtener un cociente menor que 16.
En nuestro caso, el cociente es 1 (menor que 16), con lo que hemos terminado el proceso. Hemos indicado los restos con dos rayas y el último cociente con una circunferencia.
3. El número en base 16 es:
(Último cociente) (Último resto) (Penúltimo resto)... (Segundo resto) (Primer resto).
Teniendo en cuenta que: 10 es A, 11 es B, 12 es C, 13 es D, 14 es E y 15 es F.
En nuestro caso,
Por tanto, el número 460 en base hexadecimal es 1CC. Es decir,
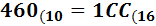
El método que seguiremos para pasar un número en base hexadecimal a base decimal es:
1. De derecha a izquierda: multiplicamos la primera cifra por 1 (1 es 16 elevado a 0); la segunda, por 16 (16 es 16 elevado a 1); la tercera, por 16 elevado a 2; la cuarta, por 16 elevado a 3. Y así hasta que hayamos multiplicado todas las cifras.
2. Sumamos cada uno de los valores obtenidos.
Ejemplo: pasamos el número A37F a base 10:
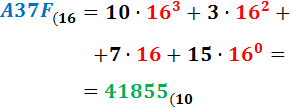
Enlaces:


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Exclusive content for members of

Mira un ejemplo de lo que te pierdes
Categories:
Tags:
Fecha publicación: 18.4.2017
The original license is kept.
Add to Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comment
0