
Cargando...
What can I do?
226539 materialEducativo
textoFiltroFichatipo de documento Mathematics - Tutorial
About this resource...
El cálculo diferencial básico (nivel bachillerato) nos permite resolver problemas de optimización. En estos problemas, se desea encontrar los puntos de máximos y/o mínimos de una función, es decir, se maximiza o minimiza una función.
Ejemplo de problema: Encontrar parejas de números x e y tales que y sea el doble del cuadrado de x y que la resta de sus cuadrados (x^2 - y^2) sea máxima.
La función que debe optimizarse en este problema es f(x) = x^2 - y^2.
Método de resolución
Para resolver este tipo de problemas, seguiremos el siguiente esquema:
Resolución del problema del ejemplo:
La función que debemos maximizar es f(x) = x^2-y^2. Esta función tiene dos variables, pero como y debe ser el doble de x^2, tenemos que y = 2x^2. Sustituimos en la función:
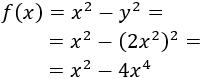
Derivamos:
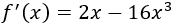
Puntos críticos:
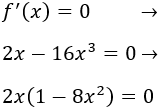
Los puntos críticos son x = 0 y
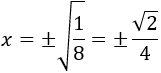
Analizando la monotonía, la función tiene máximos en los puntos
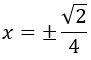
Por tanto, las parejas de números que buscamos son
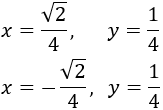
Otros temas de cálculo diferencial:
Exclusive content for members of

Mira un ejemplo de lo que te pierdes
Categories:
Fecha publicación: 21.11.2017
The original license is kept.
Add to Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comment
0