Cargando...
What can I do?
226314 materialEducativo
textoFiltroFichatipo de documento Mathematics - Tutorial
About this resource...
Un número complejo, z, es una suma de dos números:
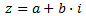
donde a es la parte real y b la parte imaginaria.
El conjunto de los números complejos contiene al de los reales:
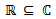
Notemos que el cuadrado de i es un real negativo:
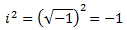
La suma de complejos es
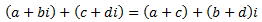
El conjugado del complejo a+bi es a-bi.
El módulo del complejo a+bi es
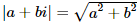
El producto es
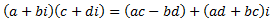
El cociente es
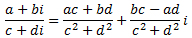
Seal los complejos z = a+bi, w = c+di y w =e+fi
1. Conjugado del conjugado:
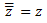
2. Conjugado de la suma:
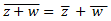
3. Producto por su conjugado:
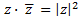
4. Conjugado del producto:
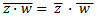
5. Conjugado del cociente:
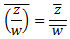
6. Módulo de un complejo:
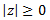
7. Módulo del conjugado:
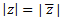
8. Módulo del producto:
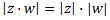
9. Módulo del inverso:
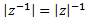
10. Módulo del cociente:
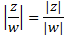
11. Desigualdad triangular (versión complejos):
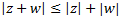
Las raíces n-ésimas de un complejo z = a + bi son
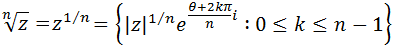
siendo
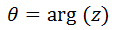
y |z| el módulo de z.
Aplicando la fórmula de Euler, las raíces son
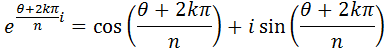
Las raíces n-ésimas de los complejos forman polígonos regulares de n lados.
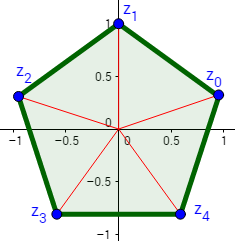
Por ejemplo, las raíces 5-ésimas del complejo z = 0 + i son
Exclusive content for members of
Mira un ejemplo de lo que te pierdes
Categories:
Tags:
Fecha publicación: 11.2.2018
The original license is kept.
Add to Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comment
1