
Cargando...
What can I do?
226539 materialEducativo
textoFiltroFichatipo de documento Mathematics - Tutorial
About this resource...
Algunas primitivas se obtienen directamente a partir de la tabla de derivadas, este es el caso de las integrales directas o inmediatas, como por ejemplo:
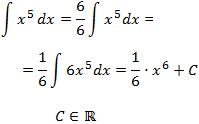
Sin embargo, lo habitual es que resolver una integral no sea una tarea fácil, razón por la que existen distintos
métodos de integración. Los métodos básicos son:
Veamos un ejemplo de cada uno de ellos:
1. Integración por partes
El método consiste en aplicar la siguiente fórmula:
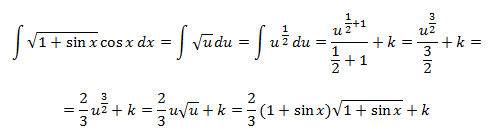
Debemos identificar en el integrando los factores u y dv.
Obtenemos du derivando u, y obtenemos v integrando dv.
Ejemplo:
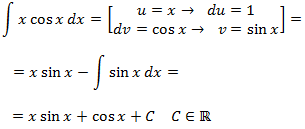
Pero la resolución de la integral dependerá de la elección de u y dv.
2. Integración por sustitución
El método consiste en aplicar un cambio de variable para conseguir en el integrando una función multiplicada por su derivada. De este modo, el resultado es dicha función.
Ejemplo:
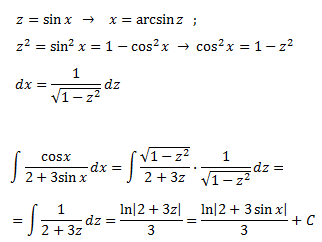
Nota: para calcular dx, se aísla x en el cambio de variable (x = arcsin(z)) y se deriva en la igualdad: se deriva respecto de x en el lado izquierdo y respecto de z en el lado derecho. Después, se aplica el cambio en el integrando, lo que supone además, cambiar dx por la expresión calculada en función de z.
Cambios de variable recomendados:

3. Integración de funciones racionales
Las integrales de funciones racionales se resuelven, generalmente, descomponiendo la fracción como suma de fracciones más simples.
Según el tipo de cociente que tengamos, deberemos descomponer la fracción de un modo u otro.
Puesto que se trata de un método cuya explicación es más extensa, proporcionamos el siguiente enlace donde podemos encontrarlo: integración de funciones racionales.
Ejemplo:
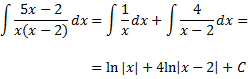
Enlaces:
Cálculo diferencial:


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

Mira un ejemplo de lo que te pierdes
Autores:
Categories:
Tags:
Fecha publicación: 9.2.2017
Content licensed under a Creative Commons Attribution 3.0 License. 
Add to Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comment
0