
Cargando...
What can I do?
226539 materialEducativo
textoFiltroFichatipo de documento Mathematics - Tutorial
About this resource...
A logarithmic equation is an equation that has an unknown factor in the argument of a logarithm. In reality, the resolution is reduced to the resolution of equations of the same type as the expressions in the arguments (quadratic equations, cubic equations, irrational equations...).
This document is a collection of resolved exercises of equations and equation systems of this kind, which are intended to be in order of increasing difficulty.
In the majority of logarithms the base is not specified, because we suppose it's 10. Although, in this sense, we must decide that in the majority of scientific texts, if it does not say otherwise, that the base is e (as it's known, Napierian logarithm).
Example 1: logarithmic equation
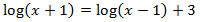
We use the logarithmic properties and we write 3 as log(1000) to obtain an equality between logarithms:
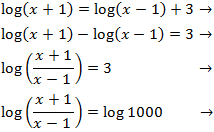
The logarithms are worth the same when their arguments (what's inside) are the same

We resolve the equation:
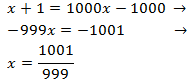
Now we have to prove that for these values of x the arguments are not 0 nor negative. But x+1 = 1001/99 > 0.
Therefore, it is the solution.
Example 2: logarithmic equation
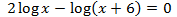
In this equation, when applying the properties to obtain an equality of logarithms, we will need to resolve a quadratic equation:
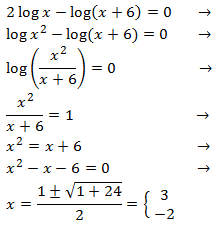
Notice that the only possible solution is x = 3 due to the fact that the arguments have to be positive.
Example 3: logarithmic equation system
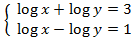
We apply the change of variable
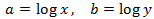
This way we obtain the following linear equation system
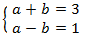
we resolve it and we undo the cange of variable:
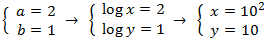
Others:
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Exclusive content for members of
Mira un ejemplo de lo que te pierdes
Categories:
Tags:
Fecha publicación: 6.2.2017
The original license is kept.
Add to Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comment
0