
Cargando...
¿Qué puedo hacer?
226539 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Acerca de este recurso...
Una sucesión es alternada cuando cada término tiene el signo contrario que el del término que le precede.
Una sucesión es oscilante cuando:
Nota: si eliminamos el primer punto de la definición de sucesión oscilante, tenemos que las sucesiones alternadas son un tipo particular de las oscilantes.
Ejemplo 1: La sucesión a(n)=n·(-1)^n es alternada. Calculamos sus primeros términos:
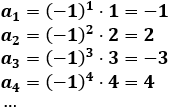
Observad que los signos se alternan: negativo, positivo, negativo, positivo...
Representación de la sucesión (n≤10):
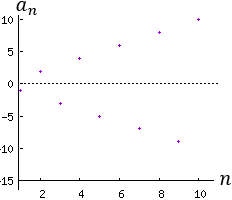
La potencia (−1)^n es positiva cuando n es par y negativa cuando n es impar. Es el causante de la alternancia del signo. La sucesión no es convergente.
Ejemplo 2: La sucesión a(n) = (-1)^n/n es alternada y convergente:
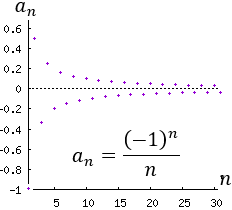
Ejemplo 3: La sucesión a(n) = -1 si n es par y a(n) = 5 si n es impar es alternada. Calculamos los 10 primeros términos:
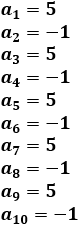
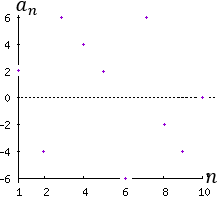
Ejemplo 4: La sucesión 2, -4, 6, 4, 2, -6, 6, -2, -4, 0, -2, 2,... es oscilante. Representación de la sucesión (n≤10):
Recursos de sucesiones o progresiones:
Contenido exclusivo para miembros de

Mira un ejemplo de lo que te pierdes
Categorías:
Fecha publicación: 19.6.2018
Se respeta la licencia original del recurso.
¿Quieres comentar? Regístrate o inicia sesión
Añadir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0