
Cargando...
¿Qué puedo hacer?
226300 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Acerca de este recurso...
De forma no rigurosa, una subsucesión de la sucesión a(n) es una sucesión que está dentro de la sucesión a(n).
Ejemplo: La sucesión de los números pares es a(n)=2n.
Una subsucesión de a(n) es la sucesión de las potencias de dos: b(n) = 2^n.
Los primeros términos de a(n) son
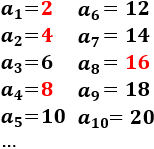
En rojo hemos indicado las potencias de 2, que son los términos de la subsucesión b(n).
Los primeros términos de b(n) son
b(1) = 2 = a(1)
b(2) = 2^2 = 4 = a(2)
b(3) = 2^3 = 8 = a(4)
b(4) = 2^4 = 16 = a(8)
b(5) = 2^5 = 32 = a(16)
...
b(n) = 2^n = a(2^(n-1))
Nota: las subsucesiones de a(n) deben estar compuestas por infinitos términos de a(n). Por ejemplo, la sucesión constante c(n) = 2 = a(1) no es una subsucesión de a(n) porque sólo está formada por un término de a(n).
Propiedades más destacadas de las subsucesiones:
Problema 1: Sea la sucesión alternada dada por
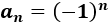
Demostrar que no converge a partir de sus subsucesiones.
Solución: La sucesión es alternada y sus primeros términos son
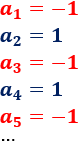
Sean las subsucesiones
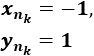
Son sucesiones convergentes porque son constantes, pero sus límites son distintos. Por tanto, a(n) no converge.
Problema 2: Sea la sucesión alternada dada por
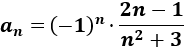
Calcular el límite de las siguientes subsucesiones de a(n):
Solución: La sucesión a(n) es alternada, pero es convergente a 0 ya que la fracción tiende a 0:
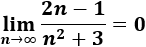
Los términos de a(n) van cambiando de signo, pero aproximándose a 0.
Como consecuencia de la convergencia de a(n), todas las subsucesiones de a(n) convergen también a 0.
Más problemas: Subsucesiones: concepto, propiedades y problemas resueltos Otros recursos de sucesiones:
Otros:
Contenido exclusivo para miembros de

Mira un ejemplo de lo que te pierdes
Categorías:
Etiquetas:
Fecha publicación: 20.6.2018
Se respeta la licencia original del recurso.
¿Quieres comentar? Regístrate o inicia sesión
Añadir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0