
Cargando...
¿Qué puedo hacer?
226539 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Acerca de este recurso...
Un sistema de ecuaciones lineales es un conjunto de ecuaciones (lineales) que tienen más de una incógnita. Las incógnitas aparecen en varias de las ecuaciones, pero no necesariamente en todas. Lo que hacen estas ecuaciones es relacionar las incógnitas entre sí. Para resolver un sistema, disponemos de varios métodos. Nosotros vamos a ver el de reducción, el de igualación y el de sustitución.
Consiste en operar con las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca. Así obtenemos una ecuación con una sola incógnita.
Ejemplo:

Para sumar las ecuaciones y que desaparezca una de las dos incógnitas, los coeficientes de dicha incógnita deben ser iguales pero de signo distinto. Para ello,
multiplicamos por -2 la primera ecuación.Después, sumamos las ecuaciones y resolvemos la ecuación obtenida:
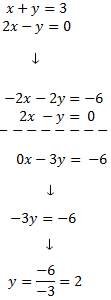
Finalmente, sustituimos el valor de y = 2 en la primera ecuación y la resolvemos:
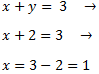
Por tanto, la solución del sistema de ecuaciones es
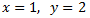
Consiste en aislar en ambas ecuaciones la misma incógnita para poder igualar las expresiones, obteniendo así una sola ecuación con una incógnita.
Ejemplo:
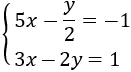
Despejamos en ambas ecuaciones la y
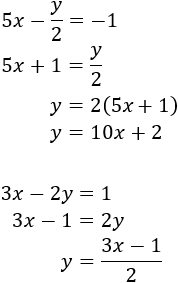
Igualamos las expresiones y resolvemos la ecuación:
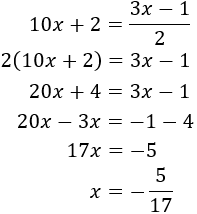
Sustituyendo x en la primera de las ecuaciones anteriores obtenemos y:
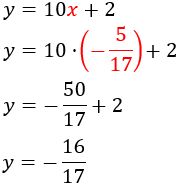
Por tanto, la solución del sistema es
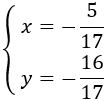
Consiste en despejar o aislar una de las incógnitas (por ejemplo, x) y sustituir su expresión en la otra ecuación. De este modo, obtendremos una ecuación de primer grado con la otra incógnita, y. Una vez resuelta, obtenemos el valor de x sustituyendo el valor de y que ya conocemos.
Ejemplo:
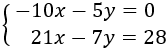
Despejamos en la primera ecuación la y:
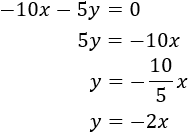
Sustituimos su expresión en la segunda ecuación y la resolvemos:
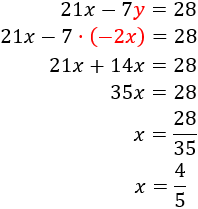
Calculamos y sabiendo x:
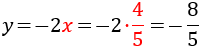
Por tanto, la solución del sistema es
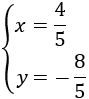
Ecuaciones de primer grado:
Contenido exclusivo para miembros de

Mira un ejemplo de lo que te pierdes
Categorías:
Etiquetas:
Fecha publicación: 15.1.2018
Se respeta la licencia original del recurso.
¿Quieres comentar? Regístrate o inicia sesión
Añadir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0