
Cargando...
¿Qué puedo hacer?
226539 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Acerca de este recurso...
La regla la usaremos para calcular límites con la indeterminación del tipo 0/0 y la de infinito dividido infinito. En realidad, como veremos en los ejemplos, podemos usarla para otro tipo de indeterminaciones.
Si tenemos las indeterminaciones
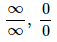
Derivamos en el numerador y en el denominador para calcular el límite.
Dicho matemáticamente (de forma no rigurosa):
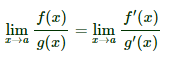
Podemos aplicar la regla tantas veces como queramos, siempre que tengamos la indeterminación cociente de infinitos o de ceros. La regla es cierta tanto para los límites con x tendiendo a un punto como a infinito.
Ejemplo 1:
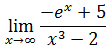
Tenemos una indeterminación del tipo infinito entre infinito. Aplicamos L’Hôpital (segunda regla)
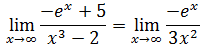
Seguimos con la misma indeterminación, y seguirá siendo mientras tengamos x en el denominador. Aplicamos la regla dos veces más:
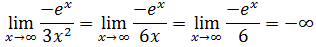
En realidad podemos calcular el límite sin aplicar L’Hôpital ya que sabemos que una exponencial crece más rápido que una función polinómica.
Ejemplo 2:
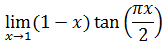
Tenemos en un principio la indeterminación cero por infinito. Pero notemos que podemos que podemos escribir el límite como
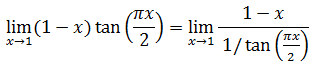
De este modo tenemos la indeterminación cero dividido cero y, por tanto, podemos aplicar L’Hôpital.
Sin embargo, para facilitar los cálculos, también podemos escribir
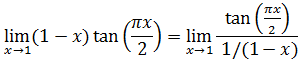
Ahora tenemos infinito dividido infinito, con lo que aplicaremos L’Hôpital, pero en este caso la derivada del denominador se calcula más rápido
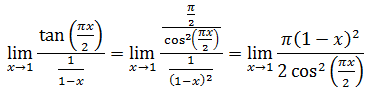
Tenemos la indeterminación cero dividido cero. Aplicamos L’Hôpita
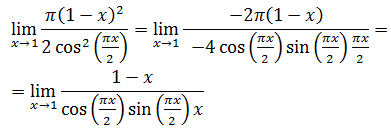
Tenemos otra vez cero dividido cero. Aplicamos L’Hôpital
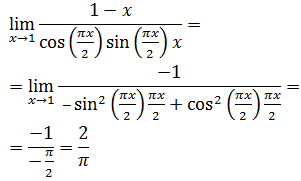
Enlaces:
Contenido exclusivo para miembros de

Mira un ejemplo de lo que te pierdes
Categorías:
Fecha publicación: 6.4.2018
Se respeta la licencia original del recurso.
¿Quieres comentar? Regístrate o inicia sesión
Añadir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0