
Cargando...
¿Qué puedo hacer?
226539 materialEducativo
textoFiltroFichaAcerca de este recurso...

1. Mínimo Común Múltiplo
Definición:
El mínimo común múltiplo de dos números a y b es el número más pequeño que es múltiplo de a y múltiplo de b.
Para denotar el mínimo común múltiplo de a y b escribiremos m.c.m.(a, b) ó mcm(a, b).
La forma más rápida de calcular el mínimo común múltiplo de dos números es:
Descomponemos los números en números primos (producto de potencias de primos).
El mínimo común múltiplo es el producto de todas las potencias que aparecen en las descomposiciones,
pero si alguna de las bases aparece en ambas descomposiciones, escogemos la de mayor exponente.
Ejemplo:
Calculamos el mínimo común múltiplo de 180 y 324.
Sus descomposiciones son:
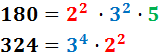
El mínimo común múltiplo tendrá las potencias de base 5, de base 3 y de base 2.
la potencia de base 2 tiene el exponente 2 en las dos descomposiciones, así que escribiremos
22
la potencia de base 3 tiene los exponentes 2 y 4. Nos quedamos con el mayor:
34
la potencia de base 5 sólo aparece en una de las descomposiciones, pero este hecho es irrelevante.
Por tanto, el mínimo común múltiplo de 180 y 324 es
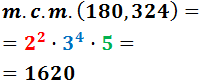
Definición:
El máximo común divisor de dos números a y b es el número más grande que divide a a y divide a b.
Para denotar el máximo común divisor de a y b escribiremos M.C.D.(a, b) ó MCD(a, b).
La forma más rápida de calcular el máximo común divisor de dos números es:
Descomponemos los números en números primos (producto de potencias de primos).
El máximo común divisor es el producto de las potencias que aparecen en las dos descomposiciones,
pero cuyo exponente sea el menor.
Ejemplo:
Calculamos el máximo común divisor de 180 y 324.
Sus descomposiciones son:
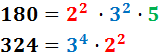
El máximo común divisor será el producto de una potencia de base 2 y otra de base 3, ya que son las bases que aparecen en las dos descomposiciones.
la potencia de base 2 tiene el exponente 2 en las dos descomposiciones, así que escribiremos
22
la potencia de base 3 tiene los exponentes 2 y 4. Nos quedamos con el menor:
32
Por tanto, el máximo común divisor de 180 y 324 es
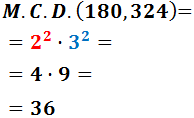
3. Referencias y Recursos
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Contenido exclusivo para miembros de

Mira un ejemplo de lo que te pierdes
Categorías:
Etiquetas:
Fecha publicación: 16.9.2016
Se respeta la licencia original del recurso.
¿Quieres comentar? Regístrate o inicia sesión
Añadir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0