1. Teorema de Pitágoras

Dado un triángulo rectángulo de catetos a y b e hipotenusa h (el lado opuesto al ángulo recto). Entonces,

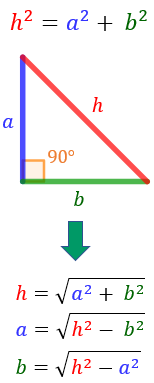
(la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa)

Recordemos que:

1. el triángulo es rectángulo porque tiene un ángulo recto, es decir, un ángulo de 90 grados ó π / 2 radianes.
2. la hipotenusa es el lado opuesto al ángulo recto

Nota: h siempre es mayor que los dos catetos, es decir, h > a y h > b.

El teorema de Pitágoras es uno de los resultados más conocidos de las matemáticas y también uno de los más antiguos. Existen cientos de demostraciones de este teorema.

2. Ejemplos de Aplicación 

2. 1. Calcular la hipotenusa del triángulo rectángulo de lados 3cm y 4cm.

Los lados son

a=3cm , b=4cm

Aplicando el teorema de Pitágoras,

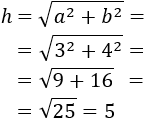
Por tanto, la hipotenusa mide 5cm.

2. 2. Calcular la altura del siguiente triángulo sabiendo que sus lados miden raíz cuadrada de 2 y raíz cuadrada de 5  y su base 3.

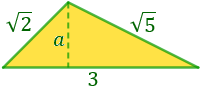
Para poder calcular la altura del triángulo, a, tenemos que dividirlo en dos triángulos rectángulos (para poder aplicar el teorema de Pitágoras).

Los dos triángulos son los siguientes:

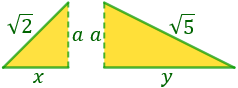
La base del triángulo (que mide 3) se divide en dos (la base de cada triángulo). No sabemos cuánto mide cada base, pero sí que sabemos que

x+y=3

Aplicamos Pitágoras al primer triángulo y obtenemos la ecuación:

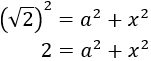
Notemos que no conocemos ninguno de los dos catetos.

Procediendo del mismo modo para el otro triángulo, obtenemos

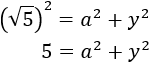
Es decir, tenemos las siguientes ecuaciones:

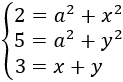
Podemos aislar la y en la tercera ecuación, obteniendo

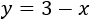
En la segunda ecuación tenemos una y, que sabemos que es 3 - x, así que sustituimos en ella:

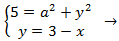
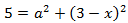
Como tenemos una resta al cuadrado, aplicamos la fórmula del binomio de Newton, que recordamos que es

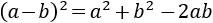
Por tanto,

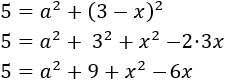
Ahora despejamos a^2 (a al cuadrado)

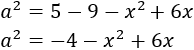
Recordemos que también teníamos la ecuación

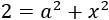
Despejamos también en ella a^2  (a al cuadrado)

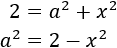
Es decir, las dos ecuaciones que tenemos son

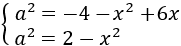
Y como a^2 = a^2, podemos igualar ambas expresiones obteniendo una ecuación de primer grado

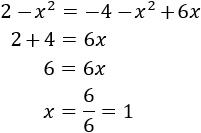
Sabiendo el valor de x podemos obtener el de y

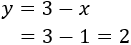
Ya sabemos cuánto mide cada base y podemos ahora calcular la altura.

La primera de las ecuaciones era

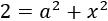
Como sabemos que x = 1 tenemos que

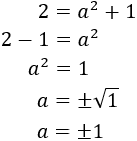
Y como a es la altura, no puede ser negativa. Por tanto, la altura del triángulo es a = 1.

3. Más información:

1. Problemas y Test de Pitágoras
2. Triángulos (clasificación)
3. Foro de ayuda 
4. Teorema de Pitàgores 
5. Pythagorean Theorem
6. Calcular porcentajes online
7. Calcular Pitágoras online
8. Problemas y Ecuaciones 
9. Ecuaciones Resueltas

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.