
Cargando...
Què puc hacer?
226539 materialEducativo
textoFiltroFichatipo de documento Matemàtiques - Tutorial
Sobre aquest recurs...
Una equació exponencial és aquella en la que apareixen exponencials, és a dir, potències que tenen la incògnita, x, en els exponents. En aquesta pàgina resoldrem equacions exponencials sense emprar logaritmes.
El mètode de resolució consisteix en aconseguir una igualtat entre dues exponencials amb la mateixa base per poder igualar els seus exponents. Aplicarem les propietats de les potències.
Exemple 1:
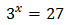
Si escrivim 27 com 3 elevat al cub, l'equació queda com
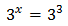
Per a que ambdues potències siguin iguals, els seus exponents han de ser iguals. Per això, la solució de l'equació és x = 3.
Exemple 2:
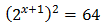
Al escriure 64 com una potència de base 2, l'equació queda com
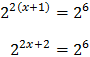
Com que ambdues potències tenen la mateixa base, igualem els exponents:
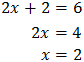
Llavors, la solució de l'equació exponencial és x = 2.
En les equacions logarítmiques, la incògnita es troba en l'argument de logaritmes. La seva resolució es redueix, en realitat, a la resolució d'equacions del mateix tipus que les expressions dels arguments (equacions de segon grau, tercer grau, irracionals...).
Per resoldre aquestes equacions, aplicarem les propietats dels logaritmes:
|
logaritme del producte:
|
|
logaritme del quocient:
|
|
logaritme de la potència:
|
|
canvi de base:
|
|
Propietat útil en la pràctica (definició de logaritme):
|
Exemple 1:
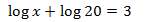
Emprarem les propietats dels logaritmes i que el logaritme de 1000 és 3:
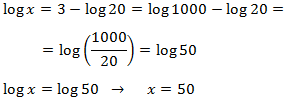
Tenim una igualtat entre logaritmes, aleshores els arguments (el de dins) han de ser els mateixos
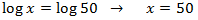
La solució de l'equació és x = 50.
Exemple 2:
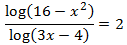
Operem en l'equació per simplificar-la. Quan tenim una igualtat entre dos logaritmes de la mateixa base, igualem els arguments. Finalment, una vegada obtingudes les solucions, comprovem que els arguments del logaritmes són positius:
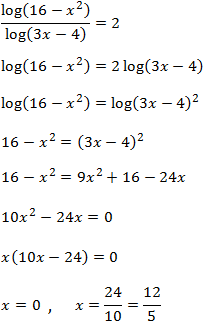
L'única solució és x = 12/5 perquè si x = 0, l'argument del logaritme del denominador és negatiu.
Més informació:

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Contingut exclusiu per a membres de

Mira un ejemplo de lo que te pierdes
Categories:
Etiquetes:
Fecha publicación: 17.2.2017
Es respecta la llicència original del recurs.
Vols comentar? Registra't o inicia sessió
Si ya eres usuario, Inicia sesión
Afegir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
2