En les equacions de primer grau la part literal dels monomis no tenen exponent major que 1 (per exemple, 3x pot aparèixer a una equació de primer grau però, x al quadrat no perquè és un monomi de segon grau). Precisament aquest fet ens assegura que, en cas d'existir solució, només n'hi ha una (excepte el cas especial en què n'hi ha infinites).

Consells a l'hora de resoldre una equació

1. Si arribem a una igualtat impossible, no hi ha solució. Per exemple, si arribem a 1 = 0 .

2. Si arribem a una igualtat que sempre es compleix, qualsevol valor per a x és solució, és a dir, la solució és "tots els nombres reals". Per exemple, si arribem a 0 = 0 .

3. Quan hi ha denominadors i volem evitar-los, podem multiplicar tota l'equació pel mínim comú múltiple d'aquests. Així, al simplificar, desapareixen.

4. Per eliminar els parèntesis, multipliquem el coeficient de davant d'aquests per tots els elements que aquests contenen. En el cas que el coeficient sigui negatiu, canviarem el signe de tots els sumands.

Exemple 1:

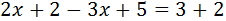
Sumem (o restem) els monomis que tenen la mateixa part literal (les x amb les x i els nombres amb els nombres). Els sumands que estan sumant a un costat passem a l'altre restant i viceversa.

Després passem les x a un costat de la igualtat i els nombres a l'altra.

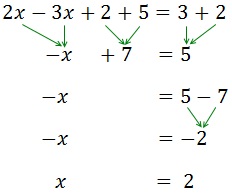
Exemple 2:

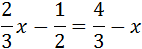
Com que hi ha denominadors, multipliquem tota l'equació pel mínim comú múltiple d'aquests, que és 6:

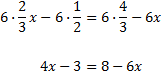
D'aquesta manera, al calcular les divisions, desapareixen els denominadors. Ara només cal agrupar les x a un costat i els nombres a l'altre.

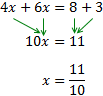
El coeficient de la incògnita, 10, està multiplicant-la. Per tant, passa a l'altre costat dividint.

Més informació:

• Resolució d'equacions de primer grau

• Problemes d'equacions de primer grau

Sistemes d'equacions

Un sistema d'equacions (lineals) és un conjunt d'equacions (lineals) que tenen més d'una incògnita. Les incògnites apareixen en diverses de les equacions però, no necessàriament en totes. El que fan aquestes equacions és relacionar les incògnites entre elles.

Per exemple,

La solució d'aquest sistema és x = 1 i y = 2 ja que per a aquests valors es compleixen les dos equacions alhora.

De la mateixa manera que una equació de primer grau pot no tenir solució, un sistema d'equacions pot també no tenir solució. Açò ocorre quan les equacions són incompatibles entre elles.

Mètodes per a resoldre un sistema:

1. Substitució: consisteix en aïllar una de les incògnites (per exemple x) i substituir la seva expressió en l'altra equació. D'aquesta manera, obtindrem una equació de primer grau amb l'altra incògnita, y. Una vegada resolta l'equació, obtenim el valor de x fent ús del valor de y que ja coneixem.

2. Reducció: consisteix en operar amb les equacions com, per exemple, sumar o restar ambdues equacions, de manera que una de les incògnites desaparegui. Així, obtenim una equació amb una sola incògnita.

3. Igualació: consisteix en aïllar en ambdues equacions la mateixa incògnita per poder igualar les expressions, obtenint així una equació amb una sola incògnita.

Exemple 1: substitució

Aïllem en la primera equació la x:

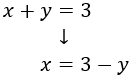
I la substituïm en la segona:

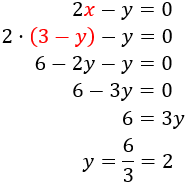
Calculem x sabent y:

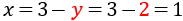
Per tant,

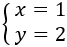
Exemple 2: igualació

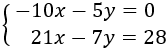
Aïllem en ambdues equacions la y

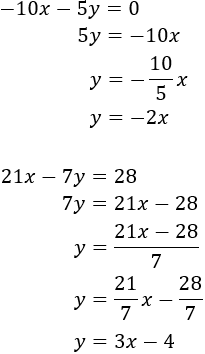
Igualem les expressions i resolem l'equació:

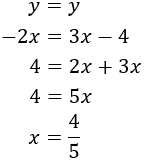
Substituïm en la primera de les equacions anteriors:

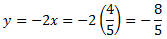
Per tant,

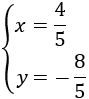
Exemple 3: reducció

Multipliquem per -2 la primera equació, sumem les equacions i resolem l'equació obtinguda:

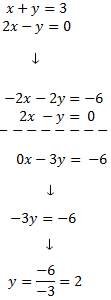
Substituïm el valor de y en la primera equació i la resolem:

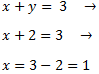
Per tant,

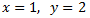
Més informació:

• Resolució de sistemes d'equacions

• Resolució de problemes amb sistemes d'equacions

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.