
Cargando...
Que pode fazer?
226300 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Sobre este recurso...
La ecuación de una recta del plano real en su forma general es y = ax + b . El coeficiente a se denomina pendiente de la recta y el coeficiente b, ordenada.
Rectas paralelas:
En el plano, dos rectas son paralelas cuando no se cortan. Es decir, cuando no tienen puntos en común.
Ejemplo: Las rectas y=2x+1 e y=2x+3 son paralelas porque no se cortan:
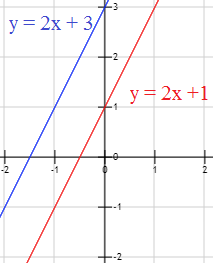
Dos rectas son paralelas si tienen la misma pendiente (coeficiente a).
Rectas perpendiculares:
Dos rectas son perpendiculares si se cortan formando un ángulo recto (un ángulo de 90 grados).
Ejemplo: las rectas y=x+2 e y=−x+2 son perpendiculares:
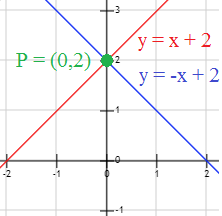
Las rectas paralelas a la recta y = ax+b son las que tiene la pendiente -1/a, es decir, son las rectas y = -x/a + k.
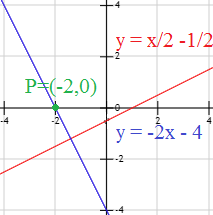
Problema: Hallar la recta que pasa por el punto P=(−2,0) y que es perpendicular a la recta y = x/2 -1/2.
Solución:
Como la ecuación está en su forma general, su pendiente es m = 1/2. La recta perpendicular a ésta debe tener la pendiente -1/m = -2. Por tanto, su ecuación será de la forma
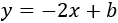
Falta calcular la ordenada b.
Como el punto P=(-2,0) es un punto de ambas rectas, sus coordenadas deben cumplir las ecuaciones.
Sustituimos las coordenadas de P en la ecuación de la recta perpendicular y resolvemos la ecuación:
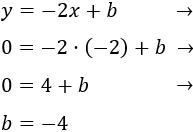
Luego la recta perpendicular es y = -2x -4.
Más problemas:
Conteúdo exclusivo para membros de

Mira un ejemplo de lo que te pierdes
Categorias:
Etiquetas:
Fecha publicación: 22.11.2017
Respeita a licença original do recurso.
Deseja fazer um comentário? Registrar o Iniciar sessão
Si ya eres usuario, Inicia sesión
Adicionar ao Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0