
Cargando...
Que pode fazer?
226539 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Tutorial
Sobre este recurso...
Per a calcular el mínim comú múltiple o el màxim comú divisor de dos o més nombres cal descompondre aquests com un producte de potències de nombres primers.
Exemple:
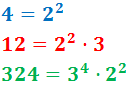
Per descompondre un nombre dividim el nombre successivament entre nombres primers fins obtenir un 1. Més concretament:
Dividim successivament per nombres primers (de manera que la divisió sigui exacta).
La descomposició és el producte de les potències dels nombres primers, els exponents dels quals indiquen les vegades que hem dividit per aquests.
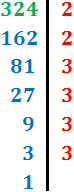
En la descomposició tenim que escriure una potència de base 2 i una potència de base 3.
Cada exponent és el nombre de vegades que es repeteix el nombre: el 2 es repeteix 2 vegades; el 3 es repeteix 4 vegades.
Per tant, la descomposició de 324 és
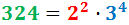
El mínim comú múltiple de dos nombres a i b és el nombre més petit que és múltiple d'a i múltiple de b. Per denotar el mínim comú múltiple d'a i b escriurem m.c.m.(a, b) ó mcm(a, b).
La manera més ràpida de calcular el mínim comú múltiple de dos nombres és:
1. Descomponem els nombres en nombres primers (producte de potències de nombres primers).
2. El mínim comú múltiple és el producte de totes les potències que apareixen en les descomposicions, però si alguna de les bases apareix en ambdues descomposicions, escrivim la de major exponent.
Aquest mètode es resumeix com
«factors comuns i no comuns al major exponent»
Exemple: Calculem el mínim comú múltiple de 180 i 324.
Les seves descomposicions són:
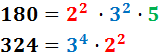
El mínim comú múltiple tindrà les potències de base 5, de base 3 i de base 2.
la potència de base 2 té l'exponent 2 en les dues descomposicions, així doncs escriurem 2 al quadrat.
la potència de base 3 té los exponents 2 i 4. Ens quedem amb el major: 3 a la quarta.
la potència de base 5 només apareix en una de les descomposicions, però aquest fet és irrellevant.
Per tant, el mínim comú múltiple de 180 i 324 és
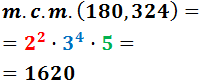
Més informació: Mínim Comú Múltiple
El màxim comú divisor de dos nombres a i b és el nombre més gran que divideix a a i divideix a b. Per denotar el màxim comú divisor d'a i b escriurem M.C.D.(a, b) ó MCD(a, b).
La manera més ràpida de calcular el màxim comú divisor de dos nombres és:
1. Descomponem els nombres en nombres primers (producte de potències de nombres primers).
2. El màxim comú divisor és el producte de les potències que apareixen en les dues descomposicions, però de tal manera que l'exponent de les quals sigui el menor possible.
Aquest mètode es resumeix com
«factors comuns al menor exponent»
Exemple:
Calculem el màxim comú divisor de 180 i 324.
Les seves descomposicions són:
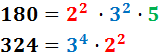
El màxim comú divisor serà el producte d'una potència de base 2 i altra de base 3, ja que són les bases que apareixen en les dues descomposicions.
la potència de base 2 té l'exponent 2 en les dues descomposicions, així doncs escriurem 2 al quadrat
la potència de base 3 té els exponents 2 i 4. Ens quedem amb el menor: 3 al quadrat.
Per tant, el màxim comú divisor de 180 i 324 és
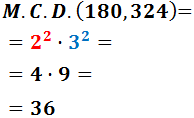
Més informació: Màxim Comú Divisor

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Conteúdo exclusivo para membros de

Mira un ejemplo de lo que te pierdes
Categorias:
Etiquetas:
Fecha publicación: 20.2.2017
Respeita a licença original do recurso.
Deseja fazer um comentário? Registrar o Iniciar sessão
Si ya eres usuario, Inicia sesión
Adicionar ao Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0