
Cargando...
Que pode fazer?
226294 materialEducativo
textoFiltroFichatipo de documento Matemáticas - Texto/Artigo
Sobre este recurso...
Una inecuación es una relación de desigualdad entre dos expresiones algebraicas en las que aparece una o más incógnitas. Resolver una inecuación consiste en encontrar todos los valores de la incógnita para los que se cumple la relación de desigualdad.
Los signos de desigualdad que se utilizan en las inecuaciones son: <, >, ≤ y ≥:
a < b significa "a es menor estrictamente que b". Por ejemplo: 2 < 3.
a > b significa "a es mayor estrictamente que b". Por ejemplo: 3 > 2.
a ≤ b significa "a es menor o igual que b". Por ejemplo: 2 ≤ 2.
a ≥ b significa "a es mayor o igual que b". Por ejemplo: 3 ≥ 2.
La solución de una inecuación es el valor o conjunto de valores que puede tomar la incógnita x de modo que se cumpla la relación.
Puede darse el caso en que la solución es sólo un punto (por ejemplo, x = 2), un intervalo (por ejemplo, [0,2]), una unión de intervalos o ninguna solución.
Una inecuación es lineal cuando las expresiones de ambos lados son polinomios de primer grado.
Ejemplo:
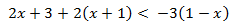
Agrupamos los monomios según su parte literal (los que tienen x y los que no) como hacemos en las ecuaciones de primer grado, pero sin multiplicar ni dividir toda la inecuación por un número negativo:
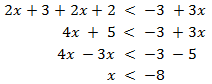
Por tanto, la solución es un intervalo:
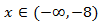
donde los paréntesis indican que los extremos del intervalo no están incluidos (desigualdad estricta).
Una inecuación es de segundo grado cuando las expresiones de ambos lados son polinomios de grado menor o igual que dos.
Ejemplo:
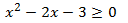
Primero calculamos los valores para los que se cumple la igualdad. Para ello, cambiamos la desigualdad por una igualdad. De este modo tendremos una ecuación de segundo grado cuyas raíces determinan los extremos de los intervalos de las soluciones de la inecuación:
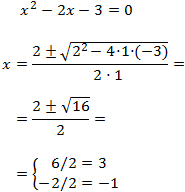
Situamos las raíces en la recta real y obtenemos 3 intervalos:
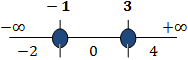
Escogemos un número al azar de cada intervalo (por ejemplo, x = -2, x= 0 y x = 4) y comprobamos si para alguno de estos valores se cumple la inecuación. No importa cuál escogemos puesto que el signo de la inecuación se mantiene constante en cada intervalo.
Comprobamos:
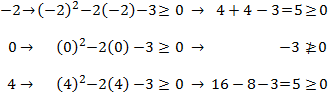
Por tanto, la inecuación se verifica en dos de los intervalos:
![x pertenece a la unión de los intervalos (-infinito, -1] y [3, + infinito) inecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). Bachiller. Bachillerato.](https://www.matesfacil.com/ESO/inecuaciones/inecuacionB1-4.png)
donde los corchetes indican que los extremos de los intervalos están incluidos (es en ellos donde se da la igualdad de la inecuación).
Una inecuación es racional cuando las expresiones de uno o ambos lados son un cociente de polinomios.
Ejemplo:
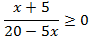
Tenemos una fracción y queremos estudiar su signo. Como estamos dividiendo, el signo de la fracción depende de los signos del numerador y del denominador.
Cuando el numerador y el denominador tienen el mismo signo, la fracción es positiva. Si lo tienen distinto, es negativa. Tenemos que ver las distintas posibilidades. Primero analizamos los signos del numerador y del denominador por separado.
Numerador:
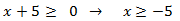
Denominador:
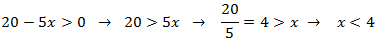
La segunda desigualdad es estricta (sin el igual) ya que el denominador no puede ser 0.
Representamos los valores en dos rectas indicando el signo en cada intervalo:
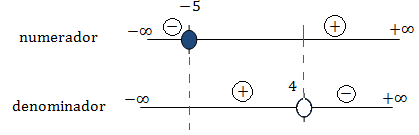
Hemos dibujado una recta encima de otra porque ahora tenemos que trabajar con ambas.
El único intervalo para el que el numerador y el denominador tienen el mismo signo (y por tanto, la solución de la inecuación) es:
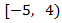
Siendo ambos positivos en el intervalo. El corchete indica que se incluye el extremo del intervalo ya que en él es donde se cumple la igualdad de la inecuación.
Enlaces:


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Conteúdo exclusivo para membros de

Mira un ejemplo de lo que te pierdes
Categorias:
Etiquetas:
Fecha publicación: 29.4.2017
Respeita a licença original do recurso.
Deseja fazer um comentário? Registrar o Iniciar sessão
Si ya eres usuario, Inicia sesión
Adicionar ao Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0