Cargando...
Que podo facer?
tipo de documento Lecciones
Un número entero es un elemento del conjunto numérico que contiene los números naturales , sus opuestos y el cero.
El conjunto de enteros incluye números ordinarios (0,1,2, ...), junto con sus opuestos (-0, -1, -2, ...). -0 y 0 se consideran iguales. Un conjunto de enteros Z generalmente recibe su nombre de la letra de la palabra alemana " Zahlen ". Los números enteros se pueden sumar, restar y multiplicar: el resultado siempre será un número entero.
La solución de las ecuaciones de tipo x + a = b, donde ayb son números enteros, será un número entero. En el caso de los números ordinarios, no ocurre lo mismo. Más rigurosamente, después de definir el conjunto de números enteros, operaciones de suma y multiplicación, hay que decir que forma un anillo intercambiable .
El número de enteros es infinito , infinitamente contables , para ser exactos.
La recta numérica o recta real es un gráfico unidimensional o línea recta la cual contiene todos los números reales ya sea mediante una correspondencia biunívoca o mediante una aplicación biyectiva, usada para representar los números como puntos especialmente marcados, por ejemplo los números enteros mediante una recta llamada recta graduada como la entera1 ordenados y separados con la misma distancia.
Los números enteros pueden sumarse, restarse, multiplicarse y dividirse, igual que puede hacerse con los números naturales.
Sumas
La adición o suma es la operación matemática de composición que consiste en combinar o añadir dos números o más para obtener una cantidad final o total. La suma también ilustra el proceso de juntar dos colecciones de objetos con el fin de obtener una sola colección. Por otro lado, la acción repetitiva de sumar uno, es la forma más básica de contar.
El hombre neolítico ya hacía matemática elemental, por lo tanto sabía sumar; pero previamente captó la idea de restar, puesto que sus medios de subsistencia disminuían durante el año, y no le era tan fácil de reponer. Los egipcios llegaron a sumar lo que se llaman hoy, números naturales y los números fraccionarios. Los babilonios llegaron a sumar los cuadrados de los números naturales. Los chinos y los hindúes sumaron números negativos. En el Renacimiento, con el auge de la banca y del comercio, se impuso la suma de decimales, catapultada por el uso del sistema de numeración decimal.
Restas
La resta o la sustracción es una operación aritmética que se representa con el signo (−); representa la operación de eliminación de objetos de una colección. La sustracción sigue varios patrones importantes. Es anticonmutativa, lo que significa que el cambio del orden cambia el signo de la respuesta. No es asociativa, lo que significa que cuando se restan más de dos números, importa el orden en el que se realiza la resta. Restar 0 no cambia un número.
Por ejemplo, en la imagen de la derecha hay 5 − 2 manzanas; significando 5 manzanas con 2 quitadas, con lo cual hay un total de 3 manzanas
Multiplicaciones
La multiplicación es una operación binaria que se establece en un conjunto numérico. Existen dos signos para indicar esta operación entre números naturales: el aspa "×" y el punto gordo a media altura ( • ). Multiplicar una cantidad por un número consiste en sumar dicha cantidad tantas veces como indica el número.
El resultado de la multiplicación de varios números se llama producto. Los números que se multiplican se llaman factores o coeficientes, e individualmente: multiplicando (número a sumar o número que se está multiplicando) y multiplicador (veces que se suma el multiplicando).
La potenciación es un caso particular de la multiplicación donde el exponente indica las veces que debe multiplicarse un número por sí mismo. Ejemplo: 2 • 2 • 2 • 2 • 2 • 2 • = 2 6 = 64
Por ejemplo, en la imagen hay, 4 bolsas de 3 bolas cada una. Para saber cuántas bolas hay en total, debemos realizar la operación 4 x 3 (léase «cuatro multiplicado por tres» o, simplemente, «cuatro por tres») es igual a sumar tres veces el número 4 (4+4+4)
Divisiones
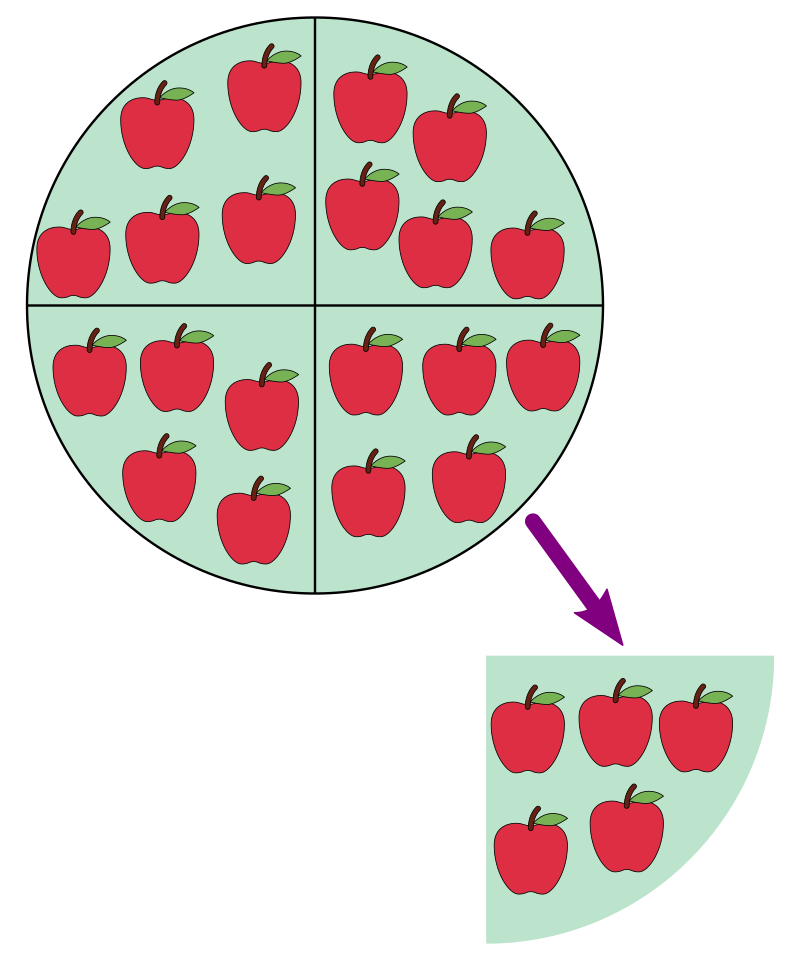En la matemática, la división es una operación parcialmente definida en el conjunto de los números naturales y los números enteros. En el caso de que sea posible efectuar la división, esta consiste en indagar cuántas veces un número (divisor) está "contenido" en otro número (dividendo). El resultado de una división recibe el nombre de cociente. De manera general puede decirse que la división es la operación inversa de la multiplicación, siempre y cuando se realice en un campo.
Debe distinguirse la división «exacta» (sujeto principal de este artículo) de la «división con resto» o residuo (la división euclídea).
A modo de ejemplo tal y como aparece en la imagen, si tenemos 20 manzanas y queremos repartirlas entre 4 personas, realizaremos la división 20 / 4 = 5 para saber cuántas manzanas tocan por persona.
Texto
Imagen
Un número entero es un elemento del conjunto numérico que contiene los números naturales , sus opuestos y el cero.
El conjunto de enteros incluye números ordinarios (0,1,2, ...), junto con sus opuestos (-0, -1, -2, ...). -0 y 0 se consideran iguales. Un conjunto de enteros Z generalmente recibe su nombre de la letra de la palabra alemana " Zahlen ". Los números enteros se pueden sumar, restar y multiplicar: el resultado siempre será un número entero.
La solución de las ecuaciones de tipo x %2b a = b, donde ayb son números enteros, será un número entero. En el caso de los números ordinarios, no ocurre lo mismo. Más rigurosamente, después de definir el conjunto de números enteros, operaciones de suma y multiplicación, hay que decir que forma un anillo intercambiable .
El número de enteros es infinito , infinitamente contables , para ser exactos.
La recta numérica o recta real es un gráfico unidimensional o línea recta la cual contiene todos los números reales ya sea mediante una correspondencia biunívoca o mediante una aplicación biyectiva, usada para representar los números como puntos especialmente marcados, por ejemplo los números enteros mediante una recta llamada recta graduada como la entera1 ordenados y separados con la misma distancia.
Los números enteros pueden sumarse, restarse, multiplicarse y dividirse, igual que puede hacerse con los números naturales.
Sumas
La adición o suma es la operación matemática de composición que consiste en combinar o añadir dos números o más para obtener una cantidad final o total. La suma también ilustra el proceso de juntar dos colecciones de objetos con el fin de obtener una sola colección. Por otro lado, la acción repetitiva de sumar uno, es la forma más básica de contar.
El hombre neolítico ya hacía matemática elemental, por lo tanto sabía sumar; pero previamente captó la idea de restar, puesto que sus medios de subsistencia disminuían durante el año, y no le era tan fácil de reponer. Los egipcios llegaron a sumar lo que se llaman hoy, números naturales y los números fraccionarios. Los babilonios llegaron a sumar los cuadrados de los números naturales. Los chinos y los hindúes sumaron números negativos. En el Renacimiento, con el auge de la banca y del comercio, se impuso la suma de decimales, catapultada por el uso del sistema de numeración decimal.
Restas
La resta o la sustracción es una operación aritmética que se representa con el signo (−); representa la operación de eliminación de objetos de una colección. La sustracción sigue varios patrones importantes. Es anticonmutativa, lo que significa que el cambio del orden cambia el signo de la respuesta. No es asociativa, lo que significa que cuando se restan más de dos números, importa el orden en el que se realiza la resta. Restar 0 no cambia un número.
Por ejemplo, en la imagen de la derecha hay 5 − 2 manzanas; significando 5 manzanas con 2 quitadas, con lo cual hay un total de 3 manzanas
Multiplicaciones
La multiplicación es una operación binaria que se establece en un conjunto numérico. Existen dos signos para indicar esta operación entre números naturales: el aspa "×" y el punto gordo a media altura ( • ). Multiplicar una cantidad por un número consiste en sumar dicha cantidad tantas veces como indica el número.
El resultado de la multiplicación de varios números se llama producto. Los números que se multiplican se llaman factores o coeficientes, e individualmente: multiplicando (número a sumar o número que se está multiplicando) y multiplicador (veces que se suma el multiplicando).
La potenciación es un caso particular de la multiplicación donde el exponente indica las veces que debe multiplicarse un número por sí mismo. Ejemplo: 2 • 2 • 2 • 2 • 2 • 2 • = 2 6 = 64
Por ejemplo, en la imagen hay, 4 bolsas de 3 bolas cada una. Para saber cuántas bolas hay en total, debemos realizar la operación 4 x 3 (léase «cuatro multiplicado por tres» o, simplemente, «cuatro por tres») es igual a sumar tres veces el número 4 (4%2b4%2b4)
Divisiones
En la matemática, la división es una operación parcialmente definida en el conjunto de los números naturales y los números enteros. En el caso de que sea posible efectuar la división, esta consiste en indagar cuántas veces un número (divisor) está "contenido" en otro número (dividendo). El resultado de una división recibe el nombre de cociente. De manera general puede decirse que la división es la operación inversa de la multiplicación, siempre y cuando se realice en un campo.
Debe distinguirse la división «exacta» (sujeto principal de este artículo) de la «división con resto» o residuo (la división euclídea).
A modo de ejemplo tal y como aparece en la imagen, si tenemos 20 manzanas y queremos repartirlas entre 4 personas, realizaremos la división 20 / 4 = 5 para saber cuántas manzanas tocan por persona.
Texto
Imagen
Contido exclusivo para membros de
Mira un ejemplo de lo que te pierdes
Categorías:
Etiquetas:
Queres comentar? Rexístrate ou inicia sesión
Si ya eres usuario, Inicia sesión
Engadir a Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comentar
0