
Cargando...
What can I do?
226539 materialEducativo
textoFiltroFichatipo de documento Mathematics - Tutorial
About this resource...
Índice
En esta página definimos corona circular y proporcionamos las fórmulas para calcular su área y su perímetro.
Una corona circular es la figura geométrica delimitada por dos circunferencias con el mismo centro (concéntricas) y radios distintos (R>r):
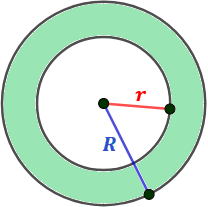
En la representación, R es el radio de la circunferencia exterior y r es el radio de la circunferencia interior.
Las fórmulas del área y del perímetro de una corona circular se obtienen a partir de las fórmulas de la circunferencia. Recordamos que el área delimitada por una circunferencia de radio R es πR^2 y su perímetro es 2πR.
Si R es el radio mayor (circunferencia exterior) y r el radio menor (circunferencia interior) de una corona circular, entonces:
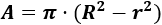
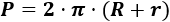
Ejemplo (Problema 1)
Calcular el área y el perímetro de una corona circular delimitada por dos circunferencias con radios 2 y 4 metros.
Solución:
El radio de la circunferencia exterior es R=4m y el radio de la circunferencia interior es r=2m. Por tanto, el área de la corona circular es
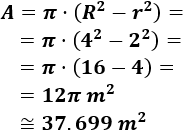
Y el perímetro es
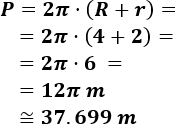
Problema 2

Una piscina con forma circular y perímetro 30π metros tiene una isla circular con un radio de 2 metros. Calcular la superficie de agua de la piscina.
Problema 3
Explicar por qué el área de una corona circular es A=π⋅(R^2−r^2) y su perímetro es P=2⋅π⋅(R+r).
Problema 4
Escribir la ecuación de una corona circular delimitada por las circunferencias con centro en el origen y radios 1 y 3.
Problema 5
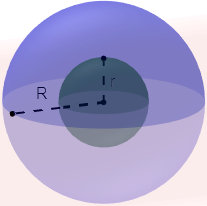
Una corona esférica es la región del espacio comprendida entre dos esferas concéntricas. ¿Cuál es su volumen?
Las soluciones a los problemas propuestos están en la página Corona circular: área, perímetro y problemas resueltos.
Otros recursos:
Exclusive content for members of

Mira un ejemplo de lo que te pierdes
Categories:
Fecha publicación: 15.7.2018
The original license is kept.
Add to Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comment
0