
Cargando...
Que puis-je faire ?
226262 materialEducativo
textoFiltroFichatipo de documento Matematiques - Tutorial
À propos de cette ressource...
When the integrand is formed by a product (or a division, which we can treat like a product) it's recommended the use of the method known as integration by parts, that consists in applying the following formula:
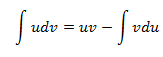
Even though it's a simple formula, it has to be applied correctly. Let's see a few tips on how to apply it well:
Select u and dv correctly: as a rule, we will call u all powers and logarithms; and dv exponentials, fractions and trigonometric functions (circular functions).
Don't change our minds about the selection: Sometimes we need to apply the method more than once for the same integral. When this happens, we need to call u the result of du from the first integral we applied the method to.
Cyclic integrals: Sometimes, after applying integration by parts twice we have to isolate the very integral from the equality we've obtained in order to resolve it. An example of this is example 3.
Example 1:
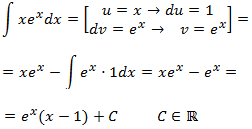
Notes: it's important to choose
x = u, so dx = du
because by doing so we're reducing the monomials degree (from 1 to 0). If we choose
x = dv, so v = x^2/2
we increase the degree (from 1 to 2) and we complicate the integral more because the exponential factor remains the same.
Example 2:
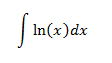
In this integral we don't have an explicit product of functions, but we don't know what the logarithms primitive function is, so we differentiate it, that way u = ln(x).
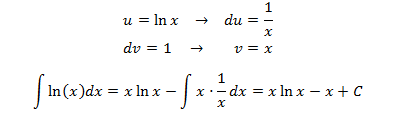
Example 3 (cyclic integral):
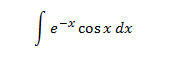
In this example it doesn't matter which factors are u and dv, because when integrating and differentiating e -x we obtain –e -x and when integrating and differentiating cos(x) we get ±sin(x). This is a cyclical integral in which we have to apply integration by parts twice (with the same choices so we don't go backwards) and we have to isolate the integral from the mathematical expression we obtain.
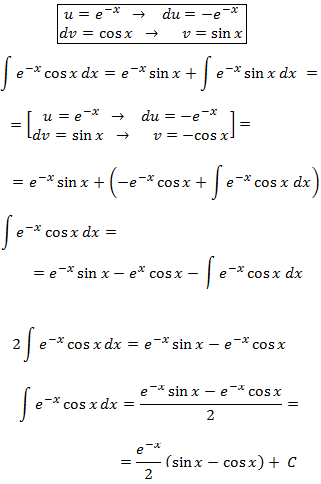
More examples: Integracion by parts method.
Others:

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Contenu exclusif pour les membres de

Mira un ejemplo de lo que te pierdes
Catégories:
Étiquettes:
Fecha publicación: 22.2.2017
La licence originale de la ressource est respectée.
Que se passe t’il ? Inscrivez-vous ou lancer session
Si ya eres usuario, Inicia sesión
Ajouter à Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Commenter
0