
Cargando...
What can I do?
226261 materialEducativo
textoFiltroFichatipo de documento Mathematics - Tutorial
About this resource...
En esta página enunciamos el teorema del emparedado (sin demostración) y lo aplicamos para calcular el límite de la función sin(x)/x cuando x tiende a infinito positivo.
El teorema del emparedado o del sándwich es un teorema que permite calcular el límite de funciones que se encuentran acotadas por otras dos funciones cuyos límites son iguales.
Se trata de un resultado muy intuitivo y existen varias versiones (para sucesiones, series, funciones con varias variables, etc.).
Sean g, f y h funciones definidas en el intervalo I que contiene al punto a tales que
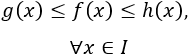
Supongamos también que
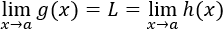
Entonces,
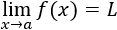
Nota: las funciones pueden no estar definidas en el punto a.
Nota 2: L debe ser finito.
Como el seno toma valores en el intervalo [−1,1],
Sólo tenemos que dividir entre x en esta relación para poder aplicar el teorema.
Como estamos calculando el límite cuando x tiende a +infinito, podemos considerar x>0 y, por tanto, podemos dividir entre x sin cambiar los signos de desigualdad:
Como el límite de -1/x y el de 1/x coinciden y es igual a 0, por el teorema del emparedado, tenemos
Nota: No podemos aplicar este mismo razonamiento para calcular el límite cuando x tiende a 0 porque los límites de las funciones utilizadas (±1/x) son distintos e infinitos. No obstante, podemos calcular su límite aplicando el mismo teorema, pero con funciones distintas.
Más ejemplos, versiones y demostración en teorema del emparedado.
Temas de límites:
Exclusive content for members of

Mira un ejemplo de lo que te pierdes
Categories:
Tags:
Fecha publicación: 25.6.2019
The original license is kept.
Add to Didactalia Arrastra el botón a la barra de marcadores del navegador y comparte tus contenidos preferidos. Más info...
Comment
2